Altitude to the hypotenuse

This geometry video tutorial provides a basic introduction into the altitude on hypotenuse theorem. When the altitude is drawn to the hypotenuse of a right triangle the altitude is the geometric mean of the hypotenuse segments pretty straight forward 2.

Draw the altitude of the hypotenuse on the triangle.

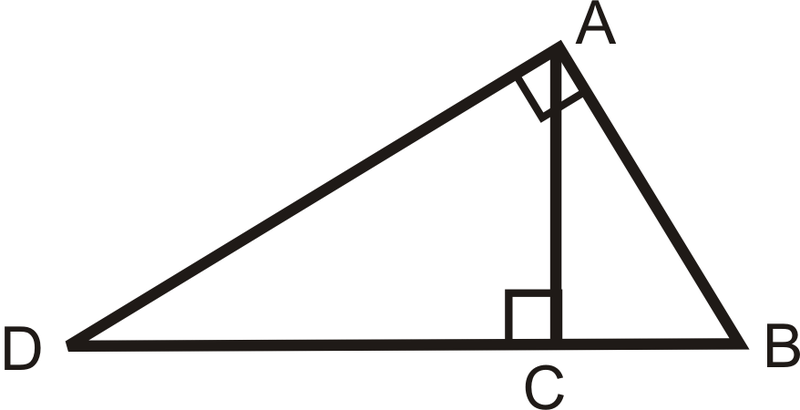
Altitude to the hypotenuse. If an altitude is drawn to the hypotenuse of a right triangle then it is the geometric mean between the segments on the hypotenuse. Use Figure 3 to write three proportions involving geometric means. Figure 3 Using geometric means to write three proportions.

Find the values for x and y in Figures 4 a through d. In a right triangle the altitude thats perpendicular to the hypotenuse has a special property. It creates two smaller right triangles that are both similar to the original right triangle.

If an altitude is drawn to the hypotenuse of a right triangle as shown in the above figure then. According to right triangle altitude theorem the altitude on the hypotenuse is equal to the geometric mean of line segments formed by altitude on hypotenuse. Which Triangle is a 30 60 90 Triangle.

Right triangleA 30-60-90 triangle is a special right triangle a right triangle being any triangle that contains a 90 degree angle that always has degree angles of 30 degrees 60 degrees and 90 degrees. In this video I will introduce you to the three similar triangles created when you construct an Altitude to the hypotenuse of a right triangle. I will go th.

First find the length of the altitude of this triangle drawn to the hypotenuse. In accordance with the formula 11 the altitude length is equal to. So the altitude length is z 6 cm.

Thus you know the legs measures in the right triangle ADC 12 cm and 6 cm. Now calculate the side a as the hypotenuse. To the Example 3.

When the altitude is drawn to the hypotenuse of a right triangle the altitude is the geometric mean of the hypotenuse segments pretty straight forward 2. CA is the geometric mean of AD and AB becomes. When the altitude is drawn to the hypotenuse of a right triangle the leg is the geometric mean of the hypotenuse segment and the hypotenuse.

AltitudeonHypotenuseTheorem2 Inanyrighttrianglethelengthofeachlegisthe geometricmeanbetweenthehypotenuseandthe segmentofthehypotenuseadjacenttothatleg. How do you find the altitude of a hypotenuse. Draw the altitude of the hypotenuse on the triangle.

The two new triangles you have created are similar to each other and the main triangle. Divide the length of the shortest side of the main triangle by the hypotenuse of the main triangle. Multiply the result by the length of the remaining side to get the length of the altitude.

When the altitude drawn from the right angle to the hypotenuse splits the hypotenuse into two sections of segments. Then the length of each leg of the right triangle is the geometric mean of the lengths of the hypotenuse and the segment of the hypotenuse that is adjacent to the leg. Hence the statement The altitude to the hypotenuse of a right triangle is the geometric mean between the segments on the hypotenuse.

The altitude to the hypotenuse of a right triangle is the geometric mean between the segments on the hypotenuse. Sometimes never always The altitude to the hypotenuse of a right triangle is Always the geometric mean between the segments on the hypotenuse. Solution for In the right triangle find the length of the altitude drawn to the hypotenuse.

The right triangle altitude theorem or geometric mean theorem is a result in elementary geometry that describes a relation between the altitude on the hypotenuse in a right triangle and the two line segments it creates on the hypotenuse. It states that the geometric mean of the two segments equals the altitude. Worksheet 1 Altitude to the Hypotenuse N ame ecz 1 If an altitude is drawn to the hypotenuse of triangle BAN below then name and redraw the 3 similar triangles created.

Find the missing value x below. 10 10 15 For 4-6 find the length of the altitude of right triangle P QR. Worksheet 1 Altitude to the Hypotenuse N ame ecz 1 If an altitude is drawn to the hypotenuse of triangle BAN below then name and redraw the 3 similar triangles created.

The length of the altitude to the hypotenuse for a 3 4 5 triangle. Answer The Question Ive Same Question Too. Depending on the orientation of the right triangle it would be between 3 and 4.

The altitude of a right triangle from its right angle to its hypotenuse is the geometric mean of the lengths of the segments the hypotenuse is split into. Using Pythagoras theorem on the 3 triangles of sides p q r s r p h and s h q. This geometry video tutorial provides a basic introduction into the altitude on hypotenuse theorem.

It explains how to find the missing sides and solve for. Find length of the altitude drawn from right angle to hypotenuse Property. A perpendicular line drawn from the vertex of a right angled triangle divides the triangle into two triangles similar to each other and also to original triangle.

What is the length of the altitude drawn to the hypotenuse. The figure is not drawn to scale. 1 point GA O TO 070 ON19 019 ms.