To use this online calculator for Apothem of a regular polygon enter Side s and Number of sides n and hit the calculate button. To find the area of the hexagon find the area of the whole triangle and multiply the value by 6 since 6 triangles can be formed in a hexagon.
In a regular hexagon split the figure into triangles.
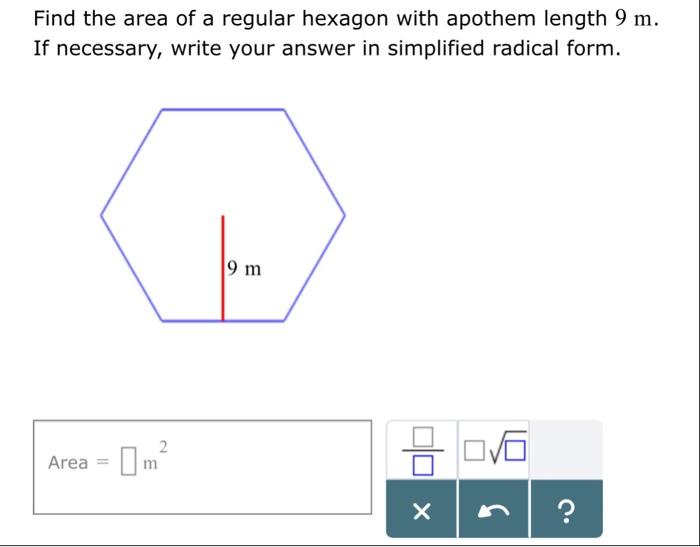
Area of hexagon with apothem. A hexagon is a six-sided polygon. When a hexagon is regular it has six equal side lengths and an apothem. An apothem is a line segment from the center of a polygon to the middle point of any one side.
You usually need to know the length of the apothem when calculating the area of a hexagon. A hexagon is a kind of polygon which has six sides and angles. A Regular hexagon has six sides and angles that are congruent and is made up of six equilateral triangles.
The formula to find out the area of a regular hexagon is as given. Area 33 s2 2 where s represent the length of a side of the regular hexagon. Write down the formula for finding the area of a hexagon with a given apothem.
The formula is simply Area 12 x perimeter x apothem. The formula for the area of a polygon is always the same no matter how many sides it has as long as it is a regular polygon. Area apothem perimeter 2.
Just as a reminder the apothem is the distance between the midpoint of any of the sides and the center. It can be viewed as the height of the equilateral triangle formed taking one side and. To find the area of the hexagon find the area of the whole triangle and multiply the value by 6 since 6 triangles can be formed in a hexagon.
Area base apothem 2 6 Area base apothem 2 123 Area base apothem 3. In a regular hexagon split the figure into triangles. Find the area of one triangle.
Multiply this value by six. Alternatively the area can be found by calculating one-half of the side length times the apothem. How to Calculate Area of a Polygon Using Apothem.
To calculate the area of a polygon with the help of apothem we use the formula. A dfrac12aP Where a apothem. Find the area of a regular hexagon if the side length is 5 inches and the apothem is 3 inches.
The area of any regular polygon is given by the formula. Area a x p2 where a is the length of the apothem and p is the perimeter of the polygon. 4 Plug the values of a and p in the formula and get the area.
As an example lets use a hexagon 6 sides with a side s length of 10. The following formula can be used to calculate an apothem of any polygon. A S 2tan180n Where a is the apothem.
S is the length of any side. Embedded content if any are copyrights of their respective owners. To find the area of an irregular polygon you must first separate the shape into regular polygons or plane shapes.
A pentagonal prism 7 faces. It has 5 rectangles on the sides and 2 pentagons on the top and bottom. The area of any polygon is given by.
Remember that the height needs to be Given ordered coordinates of a. Find the area of a regular polygon with perimeter of 44 cm and apothem length of 10 cm. As we know Area A ½ x p x a here p 44 cm and a 10 cm ½ x 44 x 10 cm 2 220 cm 2.
The apothem a can be used to find the area of any regular n-sided polygon of side length s according to the following formula which also states that the area is equal to the apothem multiplied by half the perimeter since ns p. A n s a 2 p a 2. Equilateral and equal angles ie.
Therefore the area of a regular polygon is given by. 4 Plug the values of a and p in the formula and get the area. Calculates side length inradius apothem circumradius area and perimeter.
Area of a cyclic quadrilateral. Product of the base and the height. The side lengths of an irregular polygon are also of different measure.
The area of a regular hexagon can be found if the length of any of these parts is known. Apothem side or radius. The radius of a regular hexagon is the segment drawn from the center to any of.
To see how this equation is derived see Derivation of regular polygon area formula. Given the apothem inradius If you know the apothem or inradius the perpendicular distance from center to a side. See figure above the area is given by.
Where a is the length of the apothem inradius n is the number of sides. How to calculate Apothem of a regular polygon using this online calculator. To use this online calculator for Apothem of a regular polygon enter Side s and Number of sides n and hit the calculate button.
Here is how the Apothem of a regular polygon calculation can be explained with given input values - 6193719 92tan180pi1805. Area of a Hexagon Quick Brief. To compute the location of a hexagon we separate it right into tiny six isosceles triangles.
Compute the area of triangles and after that we can increase by 6 to discover the total location of the polygon. Making Use of Perimeter and Apothem. If we understand the apothem size and perimeter of a.
So Practice problems from the Worksheet on Area of a Polygon as many times as possible so that you will understand the concept behind them. Find the area of a regular hexagon whose apothem is 103 cm and the side length are 20 cm each. Given that Hexagon apothem 103 cm.
Side length of regular hexagon 20 cm.