Area under curve trapezoidal rule

Walk through an example using the trapezoid rule then try a couple of practice problems on your own. In mathematics and more specifically in numerical analysis the trapezoidal rule is a technique for approximating the definite integral.

Approximate the integral 0 1 sin 3.

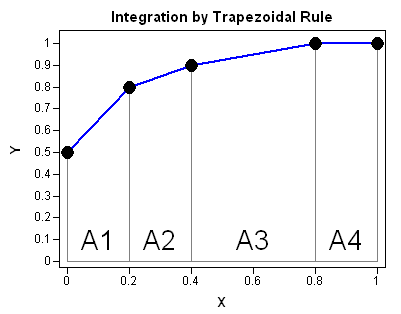
Area under curve trapezoidal rule. Its called trapezoidal rule because we use trapezoids to estimate the area under the curve. With this method we divide the given interval into n n n subintervals and then find the width of the subintervals. We call the width Δ x Delta x Δ x.

The larger the value of n n n the smaller the value of Δ x Delta x Δ x and the more accurate our final answer. With the trapezoid rule instead of approximating area by using rectangles as you do with the left right and midpoint rectangle methods you approximate area with can you guess. Because of the way trapezoids hug the curve they give you a much better area estimate than either left or right rectangles.

Trapezoidal Rule is a rule that evaluates the area under the curves by dividing the total area into smaller trapezoids rather than using rectangles. This integration works by approximating the region under the graph of a function as a trapezoid and it calculates the area. Another useful integration rule is the Trapezoidal Rule.

Under this rule the area under a curve is evaluated by dividing the total area into little trapezoids rather than rectangles. Let f x be continuous on ab. We partition the interval ab into n equal subintervals each of width.

Δx b a n such that. The trapezium rule To find the area under a curve we have to split the space into very thin strips and look at them individually. Each strip is approximately the same shape as a trapezium and we.

Example of How-to Use The Trapezoidal Rule Calculator. Calculate the area under the curve for n 8. Enter the function and limits on the calculator and below is what happens in the background.

Given that n 8 we have. Hence we will be plotting intervals are 05 gaps. Area under curve using trapezoidal Rule.

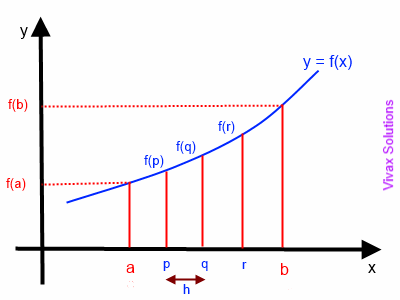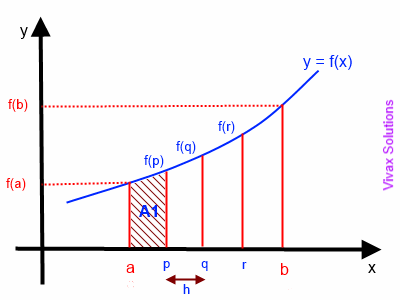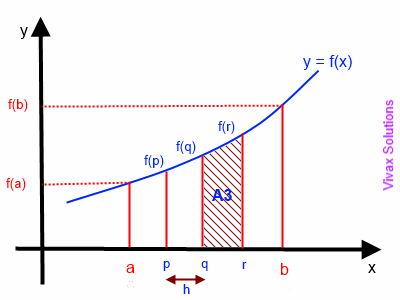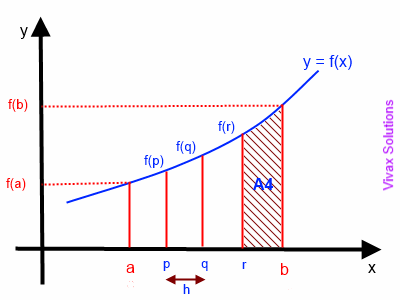
So the total area is given by. A r e a 1 2 y 0 y 1 Δ x. Displaystyletext Areaapproxfrac 1 2 left y_ 0 y_ 1rightDelta x Area 21.

The first trapezoid is between x1 and x2 under the curve as below screenshot shown. You can calculate its area easily with this formula. Then you can drag the AutoFill handle of the formula cell down to calculate areas of other trapezoids.

In the field of pharmacokinetics the area under the curve AUC is the definite integral of a curve that describes the variation of a drug concentration in blood plasma as a function of time. In practice the drug concentration is measured at certain discrete points in time and the trapezoidal rule is used to estimate AUC. Hence we just need to find the area of each trapezoid and adding them will give us total area under the curve.

R-th trapezoid of the area approximation which parallel sides of length f. Approximate the integral 0 1 sin 3. X 1 d x using n 5 trapezoids.

The trapezoidal rule states that a b f x d x Δ x 2 f x 0 2 f x 1 2 f x 2. 2 f x n 1 f x n where Δ x b a n. We have that a 0 b 1 n 5.

Therefore Δ x 1 0 5 1 5. In mathematics and more specifically in numerical analysis the trapezoidal rule is a technique for approximating the definite integral. A b f d x displaystyle int _abfdx.

The trapezoidal rule works by approximating the region under the graph of the function f displaystyle f as a trapezoid and calculating its area. It follows that a b f d x f f 2 displaystyle int _abfdxapprox cdot tfrac ff2. The trapezoidal rule may be viewed as the.

As it was highlighted in the beginning the trapezoidal rule is an approximate method to calculate the area under a curveto perform numerical integration. In the sample workbook you will notice that for the particular curve all 3 different ways that were described above result in the same value 978. Walk through an example using the trapezoid rule then try a couple of practice problems on your own.

Walk through an example using the trapezoid rule then try a couple of practice problems on your own. Over- and under-estimation of Riemann sums. Over- and under-estimation of Riemann sums.

Use trapezoidal rule to estimate the area bounded by the curve y 8 2x x 2 for -1 x 3 using 5 ordinates 4. A Using trapezoidal rule estimate the area under the curve y ½ x 2 2 between x 2 and x 8 and x-axis. So the area is approximately equal to 726 under the curve y is equal to the square root of x minus 1 between x equals 1 and x equals 6.

And we did this using trapezoids. Using trapezoidal rule to approximate the area under a curve first involves dividing the area into a number of strips of equal width. Then approximating the area of each strip by the area of the trapezium formed when the upper end is replaced by a chord.

The sum of these approximations gives the final numerical result of the area under the curve.