Calculating moment of inertia

Calculate the Moment of Inertia I of a beam section Second Moment of Area Centroid Calculator used to calculate the Centroid C in the X and Y axis of a beam section Calculate the First moment of area Statical Moment of Inertia Q of a beam section First Moment of Area A. Since the moment of inertia of an ordinary object involves a continuous distribution of mass at a continually varying distance from any rotation axis the calculation of moments of inertia generally involves calculus the discipline of mathematics which can handle such continuous variables.

This generalized relationship can be used to calculate the moment of inertia of any system since any object can be constituted as an aggregation of similar point masses.

Calculating moment of inertia. Calculating Moments of Inertia Calculate themoment of inertiafor uniformly shaped rigid bodies Apply theparallel axistheorem to find themoment of inertiaabout any axis parallel to one already known Calculate themoment of inertiafor compound objects. Summary Moments of inertia can be found by summing or integrating over every piece of mass that makes up an object multiplied. Moment of inertia is larger when an objects mass is farther from the axis of rotation.

It is possible to find the moment of inertia of an object about a new axis of. It allows you to. Calculate the Moment of Inertia I of a beam section Second Moment of Area Centroid Calculator used to calculate the Centroid C in the X and Y axis of a beam section Calculate the First moment of area Statical Moment of Inertia Q of a beam section First Moment of Area A.

For instance for a golf ball youre whirling around on a string the moment of inertia depends on the radius of the circle the ball is spinning in. Here r is the radius of the circle from the center of rotation to the point at which all the mass of the golf ball is concentrated. Basically for any rotating object the moment of inertia can be calculated by taking the distance of each particle from the axis of rotation r in the equation squaring that value thats the r2 term and multiplying it times the mass of that particle.

But for now lets look at a step-by-step guide and example of how to calculate moment of inertia. Segment the beam section into partsWhen calculating the area moment of inertia we must calculate the moment of. Calculate the Neutral Axis NAThe Neutral Axis NA or the.

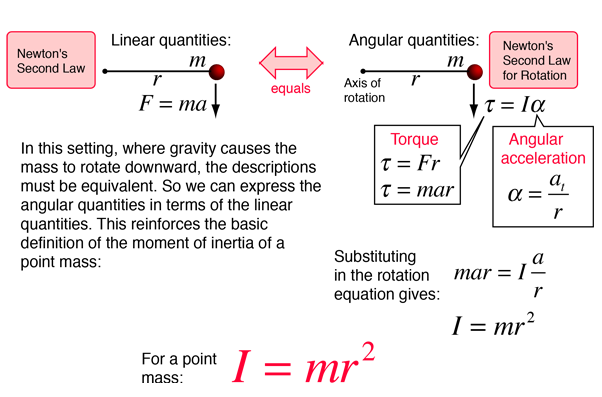
For non-uniform objects moment of inertia is calculated by the sum of the products of individual point masses and their corresponding distance from the axis of rotation. This generalized relationship can be used to calculate the moment of inertia of any system since any object can be constituted as an aggregation of similar point masses. The Moment of Inertia with respect to rotation around the z-axis of a single mass of 1 kg distributed as a thin ring as indicated in the figure above can be calculated as Iz 1 kg 1000 mm 0001 mmm2 1 kg m2 Moment of Inertia - Distributed Masses.

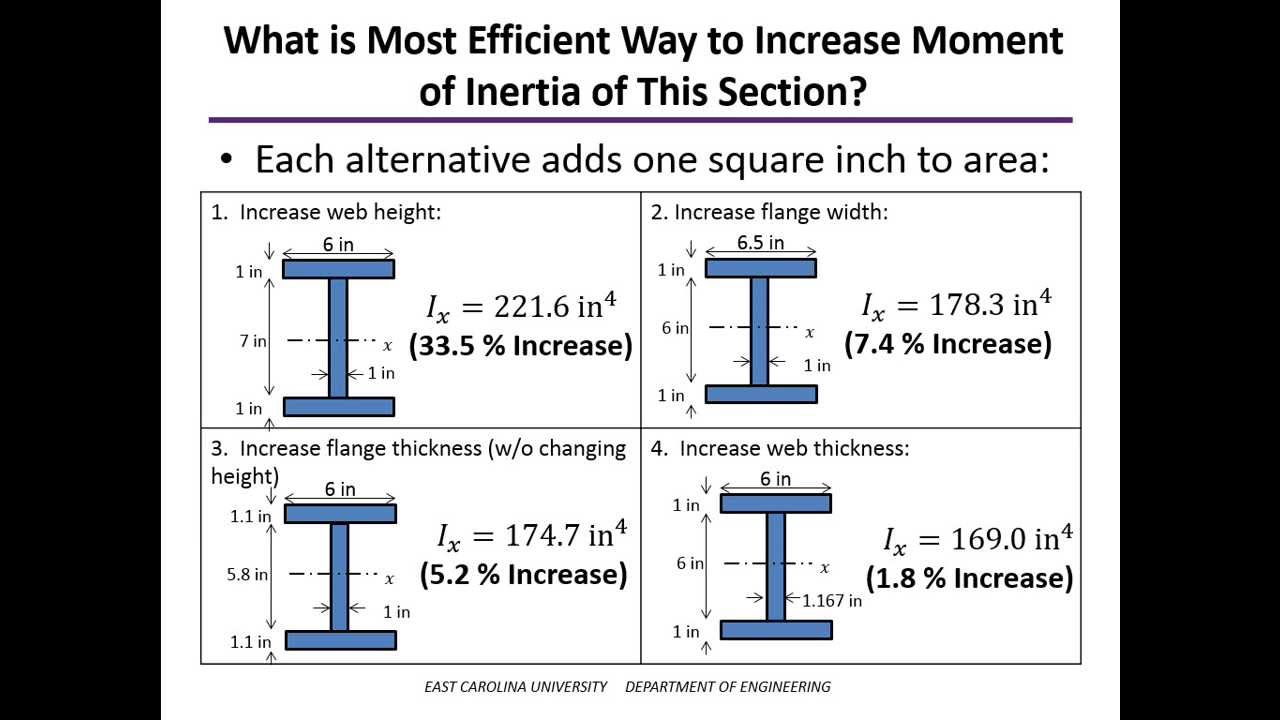
To calculate the moment of inertia of a compound shape successfully you must memorize the basic formula of the moment of inertia of basic geometric elements. These formulas are only applicable if the centroid of a basic shape coincides with the centroid of the irregular shape. Moment of Inertia and Radius of Gyration of Basic Shapes.

The torque applied to one wheel is 00020 Nm. 2 The moment of inertia of a thin rod spinning on an axis through its center is where M is the mass and L is the length of the rod. Assume a helicopter blade is a thin rod with a mass of 1500 kg and a length of 800 m.

Use double integrals to find the moment of inertia of a two-dimensional object. Use triple integrals to locate the center of mass of a three-dimensional object. We have already discussed a few applications of multiple integrals such as finding areas volumes and the average value of a function over a bounded region.

SECOND MOMENT OF AREA AREA MOMENT OF INERTIA CALCULATOR. Second Moment of Area Calculator for I beam T section rectangle c channel hollow rectangle round bar and unequal angle. Second Moment of Area is defined as the capacity of a cross-section to resist bending.

Moment of inertia may be expressed in units of kilogram metre squared kgm 2 in SI units and pound-foot-second squared lbffts 2 in imperial or US units. Moment of inertia plays the role in rotational kinetics that mass inertia plays in linear kineticsboth characterize the resistance of a body to changes in its motion. The moment of inertia depends on how mass is distributed around an axis of rotation and will vary depending on the chosen axis.

Moment of inertia denoted by I measures the extent to which an object resists rotational acceleration about a particular axis and is the rotational analogue to mass which determines an objects resistance to linear acceleration. Mass moments of inertia have units of dimension ML 2 mass length 2. Calculating the Moment of Inertia MOI sometimes called the second moment for a point mass around any axis is.

I Mr 2 where I MOI slug-ft 2 or other mass-length 2 units M mass of element Slugs or other mass unit. Moment of Inertia General Form. Since the moment of inertia of an ordinary object involves a continuous distribution of mass at a continually varying distance from any rotation axis the calculation of moments of inertia generally involves calculus the discipline of mathematics which can handle such continuous variables.

The calculation for the moment of inertia tells you how much force you need to speed up slow down or even stop the rotation of a given object. The International System of Units or SI unit of the moment of inertia is 1 kilogram per meter-squared. Symbolically this unit of measurement is kg-m2.

Here is a list of the available calculation tools relative to the moment of inertia of a shape. More accurately these tools calculate the second moment of area which is a purely geometric property of a planar shape not related to its mass.