Can you add exponents

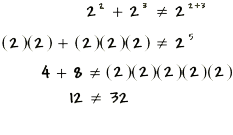
Thus the simplified version of the expression is 11x 10y. The exponent of a number says how many times to use the number in a multiplication.

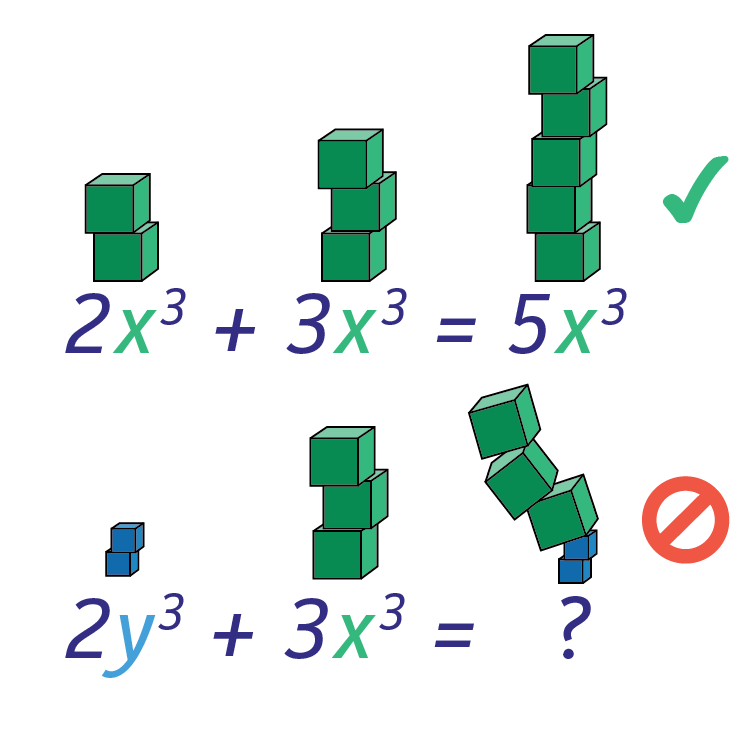
To add or subtract with powers both the variables and the exponents of the variables must be the same.

Can you add exponents. Adding fractional exponents is done by raising each exponent first and then adding. A nm b kj. 3 32 2 52 3 3 2 5 27 32 5196 5657 10853.

Adding same bases b and exponents nm. B nm b nm 2b nm. 4 23 4 23 24 23 2 3 4 2 504.

Adding variables with exponents. Adding exponents is done by calculating each exponent first and then adding. X n x m.

Adding exponents with different exponents and bases. Adding exponents is done by calculating each exponent first and then adding. The general form such exponents is.

A n b m. 4 2 2 5 4422222 1632 48. 8 3 9 2 8 8 8 9 9 512 81 593.

To add exponents start by solving the first exponential expression in the problem by multiplying the base number by itself the number of times shown in the exponent. For example to solve for 3 to the fourth power you would multiply 3 by 3 by 3 by 3 to get 81. Adding exponents and subtracting exponents really doesnt involve a rule.

If a number is raised to a power add it to another number raised to a power with either a different base or different exponent by calculating the result of the exponent term and then directly adding this to the other. The exponent product rule tells us that when multiplying two powers that have the same base you can add the exponents. In this example you can see how it works.

Adding the exponents is just a short cut. The power rule tells us that to raise a power to a power just multiply the exponents. Click to see full answer.

To add or subtract with powers both the variables and the exponents of the variables must be the same. You perform the required operations on the coefficients leaving the variable and exponent as they are. When adding or subtracting with powers the terms that combine always have exactly the same variables with exactly the same powers.

If two terms have the same variables but have different exponents they cannot be combined. In the expression 8x - 10y 3x the like terms are 8x and 3x. The sum of their numerical coefficients must be attached to the common variable and corresponding exponent.

Thus the simplified version of the expression is 11x 10y. Exponents can be added but not in the example you provided. I guess the basic understanding of multiplication and exponentiation is missing.

First of all multiplication is a short form for adding the same numbers. Instead of writing 1 1 1 1 you can write 4 1 in words four times one or to be exact add four ones to each other. If the exponents are equal then you can add or subtract the coefficients.

If the exponents are not equal you must make them equal by moving the decimal point. Moving a decimal point to the left will add to the exponent for each digit that it moves left. Once the exponents are equal you can add or subtract the coefficients.

You can add different exponents together. Your example of 2 x 4 3 x 5 illustrates this perfectly. However you cannot simplify this expression further.

In the case of 3 x 5 6 x 5 this equals 3 6 x 5 by the distributive property which simplifies to 9 x 5. Exponent rules laws of exponent and examples. What is an exponent.

What is an exponent. The base a raised to the power of n is equal to the multiplication of a n times. A n a a.

A n times. A is the base and n is the exponent. 3 1 3.

3 2 3 3 9. 3 3 3 3. The exponent of a number says how many times to use the number in a multiplication.

In 82 the 2 says to use 8 twice in a multiplication so 82 8 8 64 In words. 8 2 could be called 8 to the power 2 or 8 to the second power or simply 8 squared. The rules for adding exponents are different from adding integers whole or fractional numbers.

Here is some information about various rules to add exponents. Algebra forms one of the core areas of mathematics. Adding Exponents Property All this means is that it is an expression that is either a number a variable or a product of a number and a variable with no addition or subtraction.

And this lesson is all about multiplying two or more monomials together and simplifying them using rules for exponents. You can only add and subtract exponents when they are made of like terms That means that both the base and the power must be the same. For example take the problem 2 x2 3y x2 4 y2.

Which of these are like terms. Exponents are shorthand for repeated multiplication of the same thing by itself. For instance the shorthand for multiplying three copies of the number 5 is shown on the right-hand side of the equals sign in 5 5 5 53.

The exponent being 3 in this example stands for however many times the value is being multiplied. Simplify the given expression. Write answers with positive exponents.

Exponents are powers or indices. An exponential expression consists of two parts namely the base denoted as b and the exponent denoted as n. The general form of an exponential expression is b n.

How to Subtract Exponents. First remember that all bases have different variables so we cant add exponents together using the Product Rule. In that case using the Power Rule we can instead multiply the inner exponents with the outer exponent.

With this method we can easily and quickly see the result. X5 y9 z23 x 5 x 3 y 9 x 3 z 2 x 3.