How to calculate the altitude of a triangle

An aeroplane flies at a height of 100mm the distance of the plane from the observers point of view is 123mm. Altitude of an isosceles triangle calculator uses HeightsqrtSide A2Side B24 to calculate the Height Altitude of an isosceles triangle is a line segment through a vertex and perpendicular to a line containing the base.

Then draw a line straight to the bottom or the base of the triangle at a right angle.

How to calculate the altitude of a triangle. Recognize and name the different types of triangles based on their sides and angles. Locate the three altitudes for every type of triangle. Construct altitudes for every type of triangle.

Use the Pythagorean Theorem to calculate altitudes for equilateral isosceles and right. The altitude of a triangle is a segment from a vertex of the triangle to the opposite side or to the extension of the opposite side if necessary thats perpendicular to the opposite side. The opposite side is called the base.

You use the definition of altitude in some triangle proofs Imagine that you have. We know that the formula to find the area of a triangle is 1 2 base height 1 2 base height where the height represents the altitude. So we can calculate the height altitude of a triangle by using this formula.

H 2Area base h 2 Area base. Well-known equation for area of a triangle may be transformed into formula for altitude of a right triangle. Area b h 2 where b is a base h - height so h 2 area b.

Altitude of an Equilateral Triangle Formula. For an equilateral triangle all angles are equal to 60. In triangle ADB sin 60 hAB We know AB BC AC s since all sides are equal sin 60 hs 32 hs h 32s Altitude of an equilateral triangle h 32 s.

Click now to check all equilateral triangle formulas here. In the above triangle the line AD is perpendicular to the side BC the line BE is perpendicular to the side AC and the side CF is perpendicular to the side AB. The sides AD BE and CF are known as altitudes of the triangle.

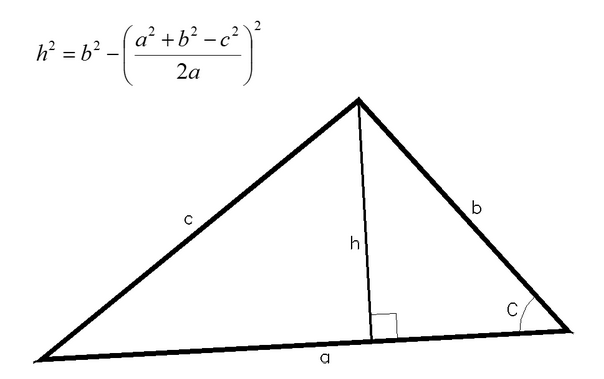
Since the sides BC and AD are perpendicular to each other the product of their slopes will be equal to -1. As usual triangle sides are named a side BC b side AC and c side AB. The altitude of a triangle to side c can be found as.

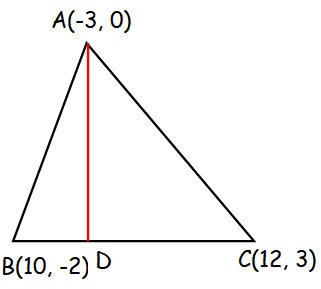
Where S - an area of a triangle which can be found from three known sides using for example Heros formula see Calculator of area of a triangle using Heros formula Altitude of a triangle. A -3 0 B 10 -2 and C 12 3 are the vertices of triangle ABC. Find the equation of the altitude through A and B.

Equation of the Medians of a Triangle Equation of the Right Bisector of a Triangle Leave a Reply Cancel reply Your email address will not be published. The altitude of a triangle is the perpendicular drawn from the vertex of the triangle to the opposite side. In an equilateral triangle all three sides are equal and all the angles measure 60 degrees.

Its altitude is calculated by the formula A 3a 2 where A is the altitude of an equilateral triangle and a is the length of the side of the equilateral triangle. Altitude of an isosceles triangle calculator uses HeightsqrtSide A2Side B24 to calculate the Height Altitude of an isosceles triangle is a line segment through a vertex and perpendicular to a line containing the base. The orthocenter of a triangle is described as a point where the altitudes of triangle meet and altitude of a triangle is a line which passes through a vertex of the triangle and is perpendicular to the opposite side therefore three altitudes possible one from each vertex.

The way to measure the altitude of this triangle is to pick a corner or vertex of the triangle. Then draw a line straight to the bottom or the base of the triangle at a right angle. An aeroplane flies at a height of 100mm the distance of the plane from the observers point of view is 123mm.

Angle of Elevation atan 100123 3911 degrees. A right triangle is a triangle with one angle equal to 90. Two heights are easy to find as the legs are perpendicular.

If the shorter leg is a base then the longer leg is the altitude and the other way round. The third altitude of a triangle may be calculated from the formula. Hᶜ area 2 c a b c.

How do you find the area of. Every triangle has 3 elevations which are also called altitudes. Attracting the height is known as going down the elevation at that vertex.

Calculate the hypotenuse of a best triangle making use of 2 sides or one side as well as one angle. And also find out the solutions for solving the hypotenuse. The ratio of the length of a side of a triangle to the sine of the angle opposite is constant for all three sides and angles.

So in the diagram below. A sine A b sine B c sine C Now you can check the sine of an angle using a scientific calculator or look it up online. Now let us calculate the altitude of the right triangle using Pythagoras theorem.

It states that in a right-angled triangle the square of the hypotenuse is equal to the sum of the squares of the other two sides ie c 2 a 2 b 2.