It can be expressed by y a where a is some constant. To find horizontal asymptotes.

If the denominators degree that is the largest exponent is greater than the numerators degree then the x-axis is the horizontal asymptote y 0.
How to find horizontal asymptotes. To Find Horizontal Asymptotes. 1 Put equation or function in y form. 2 Multiply out expand any factored polynomials in the numerator or denominator.
3 Remove everything except the terms with the biggest exponents of x found in the numerator and denominator. How To Find Horizontal Asymptotes Degree Of A Polynomial. A polynomial is an expression consisting of a series of variables and coefficients related with.
Rules For Finding Horizontal Asymptotes. Now that we have a grasp on the concept of degrees of a polynomial we can move. Finding Horizontal Asymptotes of Rational Functions If both polynomials are the same degree divide the coefficients of the highest degree terms.
If the polynomial in the numerator is a lower degree than the denominator the x-axis y 0 is the horizontal. This is always true. When the degrees of the numerator and the denominator are the same then the horizontal asymptote is found by dividing the leading terms so the asymptote is given by.
Y numerators leading coefficient denominators leading coefficient. Horizontal Asymptotes For horizontal asymptotes in rational functions the value of x x in a function is either very large or very small. This means that the terms with largest exponent in the numerator and denominator are the ones that matter.
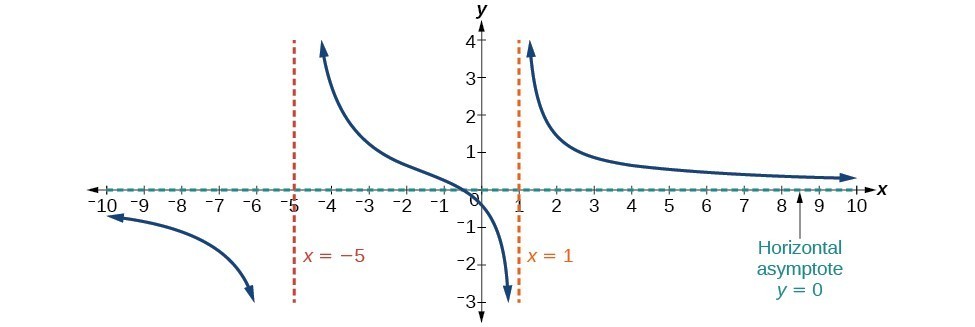
The horizontal asymptote of a rational function can be determined by looking at the degrees of the numerator and denominator. Degree of numerator is less than degree of denominator. Horizontal asymptote at y 0.
Degree of numerator is greater than degree of denominator by one. To find horizontal asymptotes you will need the following horizontal asymptote rules. If the denominators degree that is the largest exponent is greater than the numerators degree then the x-axis is the horizontal asymptote y 0.
In general we can find the horizontal asymptote of a function by determining the restricted output values of the function. If youve already learned about the limits of rational functions and limits of other functions the horizontal asymptote is simply the value returned by evaluating lim x f x. There are three types of asymptotes.
A horizontal asymptote is simply a straight horizontal line on the graph. It can be expressed by y a where a is some constant. As x goes to negative or positive infinity the value of the function approaches a.
An asymptote is a line that a curve approaches as it heads towards infinity. There are three types. Horizontal vertical and oblique.
The direction can also be negative. The curve can approach from any side such as from above or below for a horizontal asymptote. MIT grad shows how to find the horizontal asymptote of a rational function with a quick and easy rule.
Nancy formerly of MathBFF explains the stepsFor how. My Applications of Derivatives course. Use the following rules to compare those degrees and find our horizontal asymptotes.
Rule 1 If the degree of the numerator is less than the degree of the denominator then there is a horizontal. Enter the function you want to find the asymptotes for into the editor. The asymptote calculator takes a function and calculates all asymptotes and also graphs the function.
The calculator can find horizontal vertical and slant asymptotes. Next Ill turn to the issue of horizontal or slant asymptotes. Since the degrees of the numerator and the denominator are the same each being 2 then this rational has a non-zero that is a non-x-axis horizontal asymptote and does not have a slant asymptoteThe horizontal asymptote is found by dividing the leading terms.
Lets use highest order term analysis to find the horizontal asymptotes of the following functions. A The highest order term on the top is 6 x2 and on the bottom 3 x2. Dividing and cancelling we get 6 x2 3 x2 2 a constant.
Therefore the horizontal asymptote is y 2. The vertical asymptotes will occur at those values of x for which the denominator is equal to zero. X 10 x 1 Thus the graph will have a vertical asymptote at x 1.
To find the horizontal asymptote we note that the degree of the numerator is two and the degree of the denominator is one. How do you find asymptotes of an equation. Horizontal Asymptotes CAN be crossed.
To find horizontal asymptotes. If the degree the largest exponent of the denominator is bigger than the degree of the numerator the horizontal asymptote is the x-axis y 0. If the degree of the numerator is bigger than the denominator there is no horizontal asymptote.