How to find percentile in normal distribution

Z Score Positive Negative table. Std normal distribution Z table.

Z Score Positive Negative table.

How to find percentile in normal distribution. Find the corresponding percentile for Z by looking in the body of the Z -table see below and finding the probability that is closest to p from Step 1a or 1 p from Step 1b. Find the row and column this probability is in using the table backwards. This is the desired z -value.

Rearranging this formula by solving for x we get. X μ zσ confcheck 98 From our normal distribution table an inverse lookup for 99 we get a z-value of 2326. Learn how to find a percentile in a normal distribution.

Percentiles in a Normal Distribution 68-95-997 Rule Instead of always using a z-table there is also a convenient rule for estimating the probability of a given outcome. It is called the 68-95-997 Rule. Calculates the percentile from the lower or upper cumulative distribution function of the normal distribution.

The default value μ and σ shows the standard normal distribution. Normalsize Normal distribution Nxmusigma 1 probability density. Height tends to follow the normal distribution which is the case for our sample data.

The heights for this population follow a normal distribution with a mean of 1512 meters and a standard deviation of 00741 meters. For normally distributed populations you can use Z-scores to calculate percentiles. Get the free Percentiles of a Normal Distribution widget for your website blog Wordpress Blogger or iGoogle.

Find more Mathematics widgets in WolframAlpha. Percentile rank formula is used to give rank percentile of a given list in normal calculations we know the formula is R p100n1 in excel we use the rankeq function with the count function to calculate the rank percentile of a given list. Formula to Calculate Percentile Rank.

Percentile Rank is the percentage of scores that shall be equal to or it could be less than a given value or. Xnprandomnormal 25410000 sample size not mentioned in problem. I just assumed it a_9 nppercentile X10 b_9 nppercentile X90 c_9 nppercentile X80 d_9 nppercentile X50 But the answers are incorrect as per the hidden test cases of the practice platform.

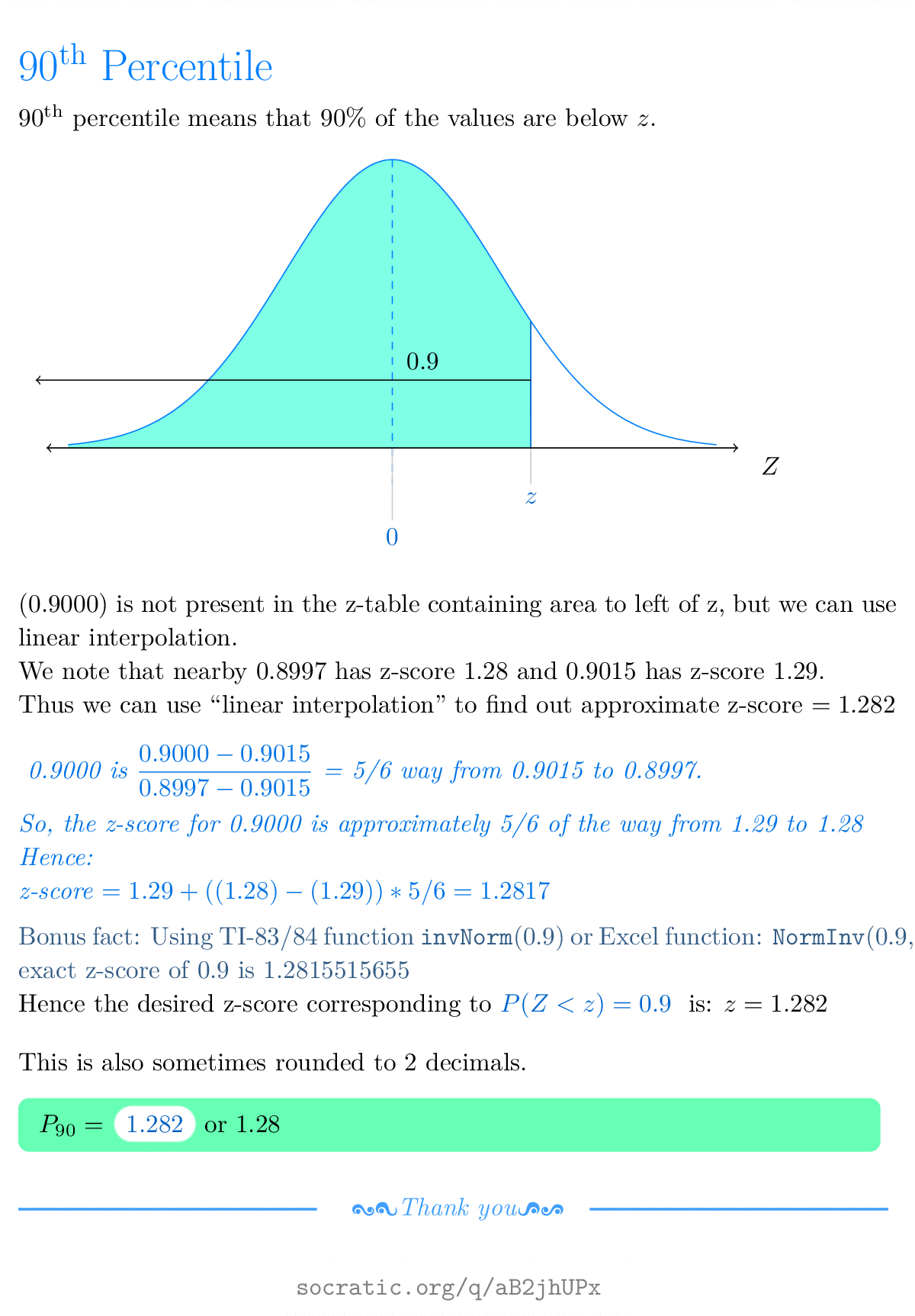
Can anyone please tell me the right way to compute the answers. First we go the Z table and find the probability closest to 090 and determine what the corresponding Z score is. For any normal distribution a probability of 90 corresponds to a Z score of about 128.

We also could have computed this using R by using the qnorm function to find the Z score corresponding to a 90 percent probability. Calculates the percentile from the lower or upper cumulative distribution function of the logarithmic normal distribution. Std normal distribution Z table.

Z Score Positive Negative table. F Distribution for α 0025. F Distribution for α 001.

Chi Square Distribution table. Negative Z Scores table. Z Score percentile table.

F Distribution for α 010. Wilcoxon Rank Sum table. Diagram showing the cumulative distribution function for the normal distribution with mean μ 0 and variance σ2 1 These numerical values 68 95 997 come from the cumulative distribution function of the normal distribution.

The prediction interval for any standard score z corresponds numerically to 1 1 Φμσ2 z2. Use the standard normal distribution to find Pz lt 196. What are the median and the mode of the standard normal distribution.

What is z value corresponding to the 65th percentile of the standard normal distribution. What is the z value such that 52 of the data are to its left. What are the 2 z values that identify the middle 50 of the standard normal distribution.

How do I use the. To compute the 90 th percentile we use the formula Xμ Zσ and we will use the standard normal distribution table except that we will work in the opposite direction. Previously we started with a particular X and used the table to find the probability.

Calculate the Percentile from Mean and Standard Deviation The most typical case when finding percentiles is the case of finding a percentile from sample data. In that case the percentile can only be estimated. But when we have population information that determines exactly the population distribution the percentiles can be computed exactly.