How to find slope of regression line

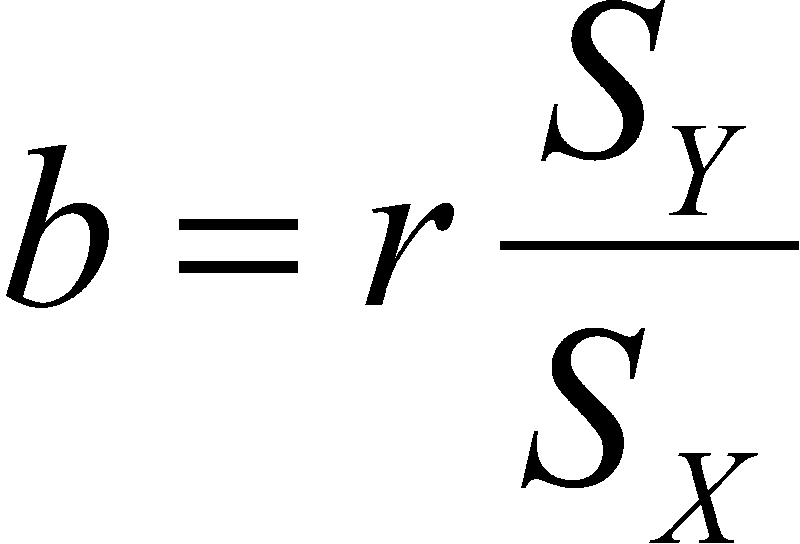
In this example the line of best. Step 1.

It explains how to find the slope and y intercept o.

How to find slope of regression line. The formula for the slope a of the regression line is. A r sysx The calculation of a standard deviation involves taking the positive square root of a nonnegative number. As a result both standard deviations in the formula for the slope must be nonnegative.

How to calculate slope and intercept of regression line. Let us see the formula for calculating m slope and c intercept. M n Σxy ΣxΣy nΣx2 Σx2.

Where n is number of observations. X input variable. Y target variable.

Let us implement a code to calculate slope of regression line. The greater the magnitude of the slope the steeper the line and the greater the rate of change. By examining the equation of a line you quickly can discern its slope and y-intercept where the line crosses the y-axis.

The slope is positive 5. When x increases by 1 y increases by 5. The y-intercept is 2.

The slope is negative 04. Finding the slope of a regression line The formula for the slope m of the best-fitting line is where r is the correlation between X and Y and sx and sy are the standard deviations of the x -values and the y -values respectively. You simply divide sy by sx and multiply the result by r.

The SLOPE function in Excel is used to calculate the slope of a line given known x and y values. The SLOPE function can be used in conjunction with the INTERCEPT function to find the equation of a linear line 1 y a bx. The SLOPE function returns the slope of the regression line created by known xs and know ys.

It is a statistical function and used in various analysis projects including regression analysis. What is the slope formula. In mathematical terms it is the number telling the steepness of the line.

The slope of the regression line is a very important part of regression analysis by finding the slope we get an estimate of the value by which the dependent variable is expected to increase or decrease. But the confidence interval provides the range of the slope values that we expect 95 of the times when the sample size is same. Predicted variable dependent variable slope independent variable intercept The slope is how steep the line regression line is.

A slope of 0 is a horizontal line a slope of 1 is a diagonal line from the lower left to the upper right and a vertical line has an infinite slope. Step 1. For each xy calculate x 2 and xy.

Xyx 2xy244835915572535710497091581135 Step 2. Sum x y x 2 and xy gives us Σx Σy Σx 2 and Σxy. M N Σ xy Σx Σy N Σ x2 Σx2 5 x 263 26 x 41 5 x 168 262 1315 1066 840.

A linear regression line has an equation of the kind. Y a bX. X is the explanatory variable Y is the dependent variable b is the slope of line a is y-intercept ie.

Value of y when x0. Regression Equation y a mx Slope m N x ΣXY - ΣX m ΣY m N x ΣX 2 - ΣX 2 Intercept a ΣY m - b ΣX m Where x and y are the variables. M The slope of the regression line a The intercept point of the regression line and the y axis.

To find the slope of a regression line or best-fitting line the formula is slope m 1n-1 x-μ x y-μ yσ x σ y σ y σ x Or if we take simplify by putting in r for the sample correlation coefficient the formula is slope m r σ y σ x. This video tutorial provides a basic introduction into the linear regression of a data set within excel. It explains how to find the slope and y intercept o.

The line fitted to the model the line fitted to model the data has a slope of 15. So the line theyre talking about is right here. So this is the scatter plot this shows that some student who spent some time in between half an hour and an hour studying got a little bit less than a 45 on the test.

We see that the intercept is 980054 and the slope is 09528. By the way lm stands for linear model. Finally we can add a best fit line regression line to our plot by adding the following text at the command line.

Abline980054 09528 Another line of syntax that will plot the regression line is. A linear regression line has an equation of the kind. A linear regression line has an equation of the kind.

Using linear regression we can find the line that best fits our data. Following data set is given. In other words for each unit increase in price Quantity Sold decreases with 835722 units.

In this example the line of best.