How to find the circumcenter of a triangle

This location gives the circumcenter an interesting property. It is also the center of the circumcircle the circle that passes through all three vertices of the triangle.

This location gives the circumcenter an interesting property.

How to find the circumcenter of a triangle. Steps to find the circumcenter of a triangle are. Calculate the midpoint of given coordinates ie. Midpoints of AB AC and BC Calculate the slope of the particular line By using the midpoint and the slope find out the equation of the line y-y1 m x-x1 Find out the equation of the other line.

Circumcenter is equidistant to all the three vertices of a triangle. The circumcenter is the centre of the circumcircle of that triangle. Circumcenter is denoted by O x y.

Image will be added soon. Multiple proofs showing that a point is on a perpendicular bisector of a segment if and only if it is equidistant from the endpoints. Using this to establish the circumcenter circumradius and circumcircle for a triangle.

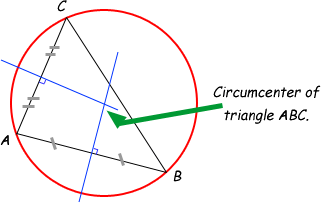
The circumcenter is the point at which the perpendicular bisectors of a triangle cross each other. It lies outside for an obtuse at the center of the Hypotenuse for the right triangle and inside for an acute. The bisectors are nothing more than the ray or thread which splits a line into two equal parts 90 degrees.

The circumcenter of a triangle can be found as the intersection of any two of the three perpendicular bisectors. The method to find circumcenter of triangle is given below. Find the midpoint of each side of the triangle.

Find the slope of line. Find the equations of the perpendicular bisectors of any two sides of the triangle. Solve the two equations found in step 2 for x and y.

The solution x y is the circumcenter of the triangle given. Method to calculate the circumcenter of a triangle Let the points of the sides be A 57 B 66 and C 2-2. Consider the points of the sides to be x1y1 and x2y2 respectively.

We need to find the equation of the perpendicular bisectors to find the points of the Circumcenter. You find a triangles circumcenter at the intersection of the perpendicular bisectors of the triangles sides. This location gives the circumcenter an interesting property.

The circumcenter is equally far away from the triangles three vertices. Find the negative inverse of that slope so you get the slope of a line parallel to a particular edge of a triangle Use the slope obtained in 3. Step and the midpoint of the corresponding edge in 1.

Step to get the vector equation of the right bisector to that edge Use two right bisectors and locate their cross section. The circumcenter of the triangle does not necessarily have to be within the triangle. It is worth noting that all triangles have a circumcircle circle that passes through each vertex and therefore a circumradius.

For the purposes of this calculator the circumradius is calculated using the following formula. In this tutorial the student will learn how to find the circumcenter of a triangle with a compass and straightedgeThis circumcenter can then be used to circ. Printable step-by-step instructions for finding the circumcenter of a triangle with compass and straightedge or ruler.

Home Contact About Subject Index. Constructing the circumcenter of a triangle. This is the step-by-step printable version.

This video shows how to construct the circumcenter of a triangle by constructing perpendicular bisectors of each side. The construction uses only a compass. In Geometry a circumcenter is defined as a point where the perpendicular bisectors of three sides of a triangle intersect.

Also it is equidistant from the three vertices of a triangle. The point of concurrency may be in on or outside of a triangle. If a triangle is an acute triangle the circumcenter is the interior of the circle.

If you want to find the circumcenter of a triangle First find the slopes and midpoints of the lines of triangle. Then perpendicular bisectors of the triangle lines Last Solve any two pair of equations The intersection point is the circumcenter. For example There points A 1 3 B 5 5 C 7 5 the circumcenter is 6 -2.

The circumcenter of a triangle is the point where the perpendicular bisectors of the sides intersect. It is also the center of the circumcircle the circle that passes through all three vertices of the triangle. The circumcenter of an obtuse triangle is outside the triangle These locational features can be seen by considering the trilinear or barycentric coordinates given above for the circumcenter.

All three coordinates are positive for any interior point at least one coordinate is negative for any exterior point and one coordinate is zero and two are positive for a non-vertex point on a side of.