How to find the exterior angle of a polygon

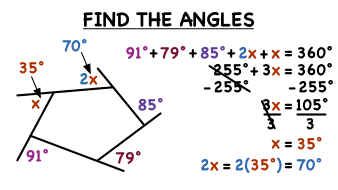
The marked angles are called the exterior angles of the pentagon. Although you know that sum of the exterior angles is 360 you can only use formula to find a single exterior angle if the polygon is regular.

Interior and exterior angle formulas.

How to find the exterior angle of a polygon. The exterior angle is 360 5 72. The interior and exterior angles add up to 180. The interior angle is 180 - 72 108.

The sum of interior angles is 5 - 2 180 540. Exterior Angles of Polygons The Exterior Angle is the angle between any side of a shape and a line extended from the next side. When we add up the Interior Angle and Exterior Angle we get a straight line 180.

They are Supplementary Angles. A Polygon is any flat shape with straight sides. The Exterior Angles of a Polygon add up to 360.

Interior and exterior angle formulas. The sum of the measures of the interior angles of a polygon with n sides is n 2180. The measure of each interior angle of an equiangular n -gon is If you count one exterior angle at each vertex the sum of the measures of the exterior angles of a polygon is always 360.

The sum of exterior angles of a polygon is 360. The formula for calculating the size of an exterior angle is. Exterior angle of a polygon 360 number of sides.

In a polygon an exterior angle is formed by a side and an extension of an adjacent side. Exterior angles of a polygon have several unique properties. The sum of exterior angles in a polygon is always equal to 360 degrees.

Therefore for all equiangular polygons the measure of one exterior angle is equal to 360 divided by the number of sides in the polygon. The following formula is used to calculate the exterior angle of a polygon. A 360 N Where A is the exterior angle N is the number of sides of the polygon.

Although you know that sum of the exterior angles is 360 you can only use formula to find a single exterior angle if the polygon is regular. Consider for instance the pentagon pictured below. Even though we know that all the exterior angles add up to 360 we can see by just looking that each angle A text and and angle B are not congruent.

An exterior angle basically is formed by the intersection of any of the sides of a polygon and extension of the adjacent side of the chosen side. Interior and exterior angles formed within a pair of adjacent sides form a complete 180 degrees angle. Measures of Exterior Angles They are formed on the outer part that is the exterior of the angle.

To find the value of a given exterior angle of a regular polygon simply divide 360 by the number of sides or angles that the polygon has. For example an eight-sided regular polygon an octagon has exterior angles that are 45 degrees each because 3608 45. Correct answer to the question.

Measure of exterior angle of regular polygon is calculated by dividing the sum of the exterior angles by the number of sides and is represented as MOE360n or Measure of exterior angle 360Number of sides. The number of Sides is used to classify the polygons. To find the value of a given exterior angle of a regular polygon simply divide 360 by the number of sides or angles that the polygon has.

For example an eight-sided regular polygon an octagon has exterior angles that are 45 degrees each because 3608 45. Solution for A regular polygon has an exterior angle that measures 9. How many sides does the polygon have.

What is the sum of the interior angles for. Exterior angle of polygons. The exterior angle of a polygon is the angle formed outside a polygon between one side and an extended side.

The measure of each exterior angle of a regular polygon is given by. Measure of each exterior angle 360n. Where n number of sides of a polygon.

Exterior and interior angles are supplementary meaning they sum to 180 degrees. If the exterior and interior angles are x and 5x respectively we can write x 5x 180 and solving for x we get x 30. This means that the answer to a is 30 and the answer to b is 30 5 150.

For c to find the number of sides we can do. 180 - 150 30. Exterior angles of a convex polygon Consider the pentagon below.

The marked angles are called the exterior angles of the pentagon. Each exterior angle is paired with a corresponding interior angle and each of these pairs sums to 180 they are supplementary. Exterior angles are created by extending one side of the regular polygon past the shape and then measuring in degrees from that extended line back to the next side of the polygon.

Since you are extending a side of the polygon that exterior angle must necessarily be supplementary to the polygons interior angle.