How to find the incenter of a triangle

The Incenter of a triangle is the point where all three angle bisectors always intersect and is the center of the triangles incircle. Calculate the incenter position then click show.

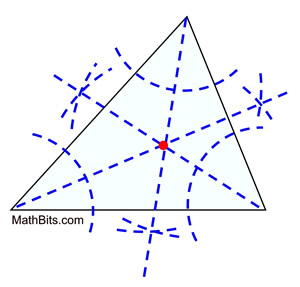
Where all three lines intersect is the center of a triangles incircle called the incenter.

How to find the incenter of a triangle. Find the coordinates of the incenter of the triangle whose vertices are A3 1 B0 1 and C-3 1. The vertices of the triangle are. A3 1 B0 1 and C-3 1 Let a be the length of the side opposite to the vertex A b be the length of the side opposite to the vertex B and c be the length of the side opposite to the vertex C.

First let us calculate the sides abc of the triangle. D x2 - x12 y2 - y12 Step 2. Substitute the abc values in the coordinates formula.

Things to try In the diagram at the top of the page Drag the points A B or C around and notice how the incenter moves and the. Drag the triangle to some random new shape. Calculate the incenter position then click show.

Area sr 90 15r 90 15 r 6 r Area s r 90 15 r 90 15 r 6 r. R 6 feet r 6 feet. The coordinates of the incenter of the triangle ABC formed by the points A31B03C31 A 3 1 B 0 3 C 3 1 is pq p q.

Find pq p q. You find a triangles incenter at the intersection of the triangles three angle bisectors. This location gives the incenter an interesting property.

The incenter is equally far away from the triangles three sides. No other point has this quality. Incenters like centroids are always inside their triangles.

This page shows how to construct draw the incenter of a triangle with compass and straightedge or ruler. The Incenter of a triangle is the point where all three angle bisectors always intersect and is the center of the triangles incircle. See Constructing the incircle of a triangle.

In this construction we only use two bisectors as this is sufficient to define the point where they intersect and we bisect the angles using the method described in Bisecting an Angle. The incenter of triangle is defined by the intersection point of angle bisectors of three vertices. It is one among the four triangle center but the only one that does not lie on the Euler line.

In other words Incenter can be referred as one of the points of concurrency of the triangle. The incenter is the point where all three of the angle bisectors of the triangle intersect. We know that this point is inside the triangle no matter the angle because all three angle bisectors are in the interior of the angles.

In a triangle A B C if A D B E C F are the angle bisectors of A B C respectively with incenter I and A 120 Find D F I Its 30. I dun know how to solve this all I could find is B I C 150 B I F 30 and D F I D E I 60. There are many methods available when it comes to discovering the sides and angles of a triangle.

To find the length or angle of a triangle one can use formulas mathematical rules or the knowledge that the angles of all triangles add up to 180 degrees. Tools to Discover the Sides and Angles of a Triangle. Given the vertices of a triangle and length of its sides.

A circle is inscribed in a triangle. The task is to find the incenter of a triangle. Learn how to construct the incenter of a triangle in this free math video tutorial by Marios Math Tutoring using a compass and straightedge.

Finding the Incenter All triangles have an incenter and it always lies inside the triangle. One way to find the incenter makes use of the property that the incenter is the intersection of the three angle bisectors using coordinate geometry to determine the incenters location. Unfortunately this is often computationally tedious.

Well to begin the incenter of a triangle is equidistant from all sides of the triangle. Essentially what he drew was the distance from the incenter to each side of the triangle which has to be perpendicular to the side it intersects. Where all three lines intersect is the center of a triangles incircle called the incenter.

Find the incenter of a triangle using a compass and straightedge at. Inscribe a Circle in a Triangle. Draw a line segment called the altitude at right angles to a side that goes to the opposite corner.

Simply construct the angle bisectors of the three angles of the triangle. The point where the angle bisectors intersect is the incenter. Actually finding the intersection of only 2 angle bisectors will find the incenter.

Finding the third angle bisector however will ensure more accuracy of the find. The incenter is one of the triangles points of concurrency formed by the intersection of the triangle s 3 angle bisectors. These three angle bisectors are always concurrent and always meet in the triangles interior unlike the orthocenter which may or may not intersect in the interior.

The incenter is the center of the incircle.