How to get the exterior angle of a polygon

As a demonstration of this drag any vertex towards the center of the polygon. A Polygon is any flat shape with straight sides.

Exterior angles of polygons.

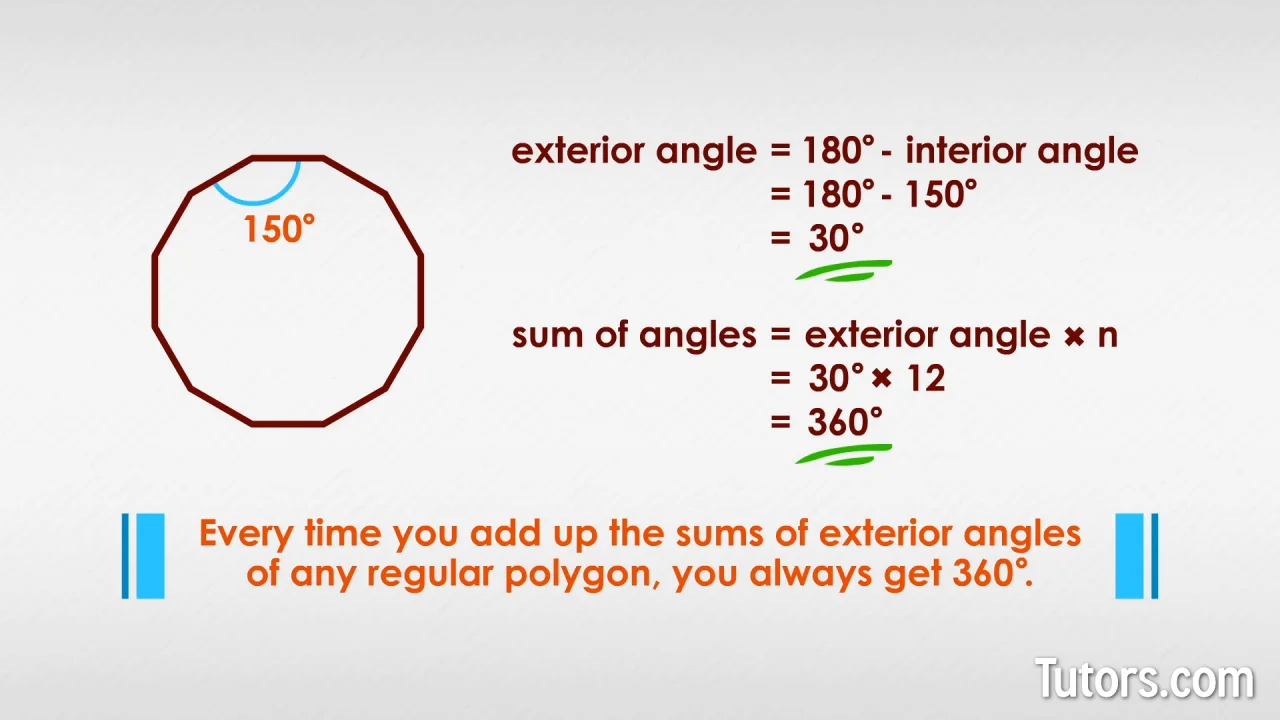
How to get the exterior angle of a polygon. Exterior Angles of Polygons The Exterior Angle is the angle between any side of a shape and a line extended from the next side. When we add up the Interior Angle and Exterior Angle we get a straight line 180. They are Supplementary Angles.

A Polygon is any flat shape with straight sides. The Exterior Angles of a Polygon add up to 360. The sum of the exterior angles of a polygon is 360.

There are as many exterior angles as there are sides n and they are all equal. The sum is divided by n to find each exterior angle. In this formula n is the number of sides of the polygon.

Refer to the figure above. It shows in detail one vertex of the polygon. You can see that the interior angle and exterior angle are supplementary adding to 180As you drag the vertex downwards the polygon becomes concave with the vertex pushed inwards towards the center of the polygonAs this happens the extended side now moves inside the polygon and the exterior angle becomes negative.

Interior and exterior angle formulas. The sum of the measures of the interior angles of a polygon with n sides is n 2180. The measure of each interior angle of an equiangular n -gon is If you count one exterior angle at each vertex the sum of the measures of the exterior angles of a polygon is always 360.

The sum of exterior angles of a polygon is 360. The formula for calculating the size of an exterior angle is. Exterior angle of a polygon 360 number of sides.

Formula for sum of exterior angles. The sum of the measures of the exterior angles of a polygon one at each vertex is 360. Measure of a Single Exterior Angle Formula to find 1 angle of a regular convex polygon of n sides.

Learn how to find the Interior and Exterior Angles of a Polygon in this free math video tutorial by Marios Math Tutoring. We discuss regular and nonregular. The sum of exterior angles in a polygon is always equal to 360 degrees.

Therefore for all equiangular polygons the measure of one exterior angle is equal to 360 divided by the number of sides in the polygon. Exterior angle sum of angles equiangular polygon. When we add up the Interior Angle and Exterior Angle we get a straight line 180.

They are Supplementary Angles. Exterior Angles of Polygons Interior Angles Interior Angles of Polygons Supplementary Angles Angles On a Straight Line Straight Angle Degrees Angle Geometry Index. How to Calculate the Sum of the Exterior Angles of a Polygon Regular Polygons.

The angles of a regular polygon are equivalent and their sides are as well. The sum of the exterior. The sum of the exterior angles of an irregular polygon also equals 360 degrees even though.

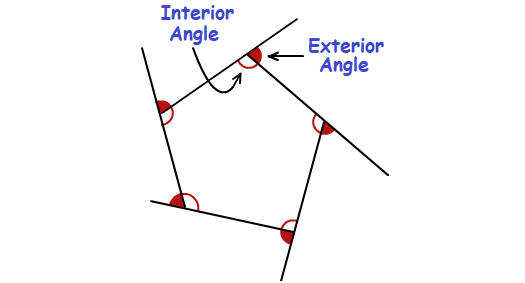
In a polygon an exterior angle is formed by a side and an extension of an adjacent side. Exterior angles of a polygon have several unique properties. The sum of exterior angles in a polygon is always equal to 360 degrees.

Therefore for all equiangular polygons the measure of one exterior angle is equal to 360 divided by the number of sides in the polygon. Exterior angles of polygons. If the side of a polygon is extended the angle formed outside the polygon is the exterior angle.

The sum of the exterior angles of a polygon is 360. Formula for the sum of exterior angles The sum of exterior angles of any polygon is 360. The exterior angle of a regular n-sided polygon is 360n Worksheet using the formula for the sum of exterior angles.

Each interior angle 144010 144 Note. Interior Angles are sometimes called Internal Angles Interior Angles Exterior Angles Degrees Angle 2D Shapes Triangles Quadrilaterals Geometry Index. Angles of a regular polygon You have already seen that the sum of the exterior angles is 360circ and that the interior and the exterior angles add up to 180circ.

A regular polygon is. As you can see for regular polygons all the exterior angles are the same and like all polygons they add to 360 see note below. So each exterior angle is 360 divided by the n the number of sides.

As a demonstration of this drag any vertex towards the center of the polygon. You will see that the angles combine to a full 360 circle. To do this divide the sum of the interior angles by the number of interior angles.

In the example above you would divide 540 by 5 because there are 5 equally sized interior angles in a.