I can easily find the asymptoties by doing y x 4 x 2 x 2 6 x 2 1 6 x 2. Graph the rational function y 4 x 1 2 x 1 The vertical asymptote of a rational function is x -value where the denominator of the function is zero.

Learn how to graph a rational function.
How to graph a rational function. Process for Graphing a Rational Function Find the intercepts if there are any. Remember that the y y -intercept is given by 0f 0 0 f 0 and we find. Find the vertical asymptotes by setting the denominator equal to zero and solving.
Find the horizontal asymptote if it exists using the. To graph a rational function you find the asymptotes and the intercepts plot a few points and then sketch in the graph. Once you get the swing of things rational functions are actually fairly simple to graph.
Lets work through a few examples. First Ill find the vertical asymptotes if any for this rational function. Find the y-values of each local extremum.
Plug the x -values from the previous step back into the original rational function to find the corresponding y -values. In the example f 32 116 and f -52 -6516. Add these points 32 116 and -52 -6516 to the graph.
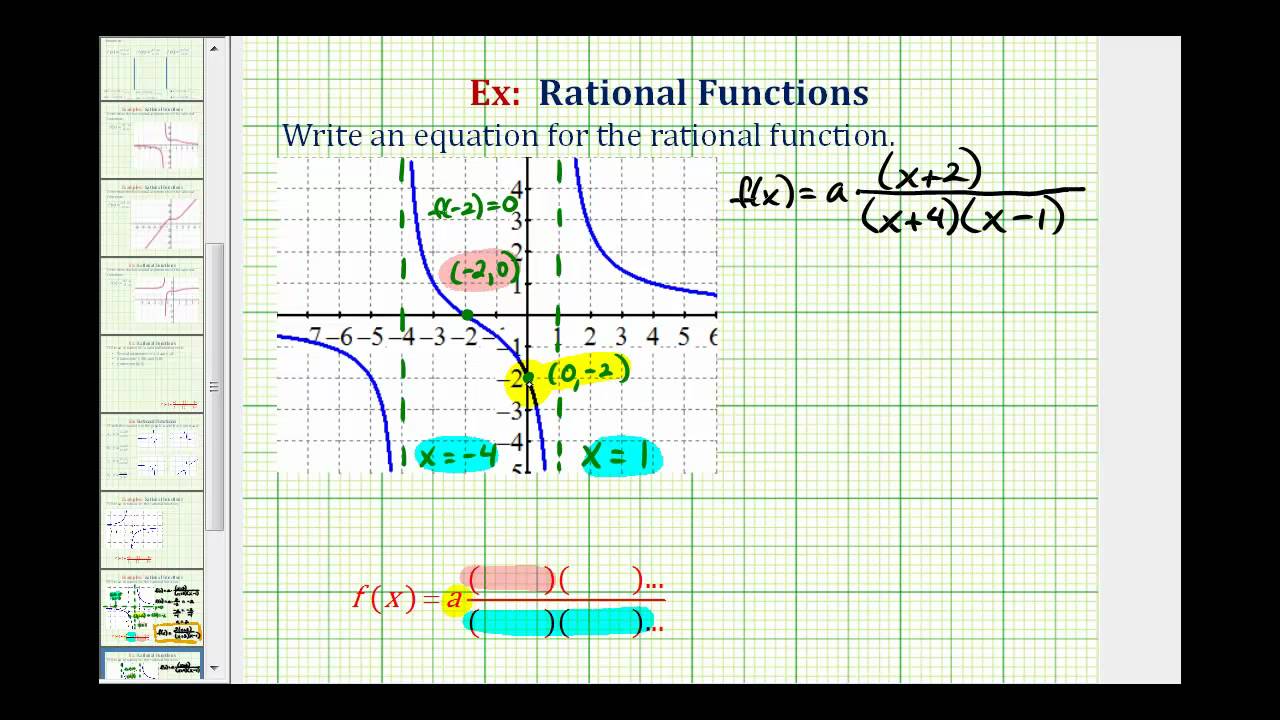
Given a graph of a rational function write the function. Determine the factors of the numerator. Examine the behavior of the graph at the x -intercepts to determine the zeroes.
Determine the factors of the denominator. Examine the behavior on both sides of each vertical asymptote to. Given a rational function sketch a graph.
Evaluate the function at 0 to find the y-intercept. Factor the numerator and denominator. For factors in the numerator not common to the denominator determine where each factor of the numerator is zero to find the x-intercepts.
Find the multiplicities of the x-intercepts to determine the behavior of the graph at those points. How to Graph Rational Functions From Equations in 7 Easy Steps 1. FACTOR the numerator and denominator 2.
See if there are any HOLES 3. Find VERTICAL ASYMPTOTES by finding where factors in the denominator equal zero 4. See if the fraction is TOP HEAVY BOTTOM HEAVY OR BALANCED for Non-Vertical.
GRAPH OF A RATIONAL FUNCTION A rational function is a function which is a fraction where both numerator and denominator are polynomials. That is a ratio of two polynomials P x and Q x where the denominator Q x is not equal to zero. Before we learn how to graph rational functions first we have to be aware of the following stuff.
Steps to How k Affects the Graph of a Rational Function. 1 Set up your table and graph. 2 Identify the shifts that will occur in your graph.
These will also be domain and range. H orginates from where y axis is being domain and k originates from where x axis is being range. To graph a rational function fx dfracpxqx we need find these important elements.
Check if the rational functions has holes. Make sure to plot these as unfilled dots. Inspect the function for any possible vertical asymptotes.
View 53 The Graph of Rational Functions-pdf from MATH P100 at Qatar University. Pre-Calculus _ Chapter 5 53. The Graph of a Rational Function Objectives.
1- Analize the Graph of a Rational. To graph a rational function is really easy. First find out the intercepts if there are any then find out the vertical asymptotes by setting the denominator equal to zero and the solving.
Find the horizontal asymptote if it exists and then sketch the graph. Written by Nitisha Sahai. Learn how to graph a rational function.
To graph a rational function we first find the vertical and horizontal asymptotes and the x and y-intercepts. To graph this function an equilateral hyperbola I have to determine the asymptoties the centre and the simmetrical axis. I can easily find the asymptoties by doing y x 4 x 2 x 2 6 x 2 1 6 x 2.
So the orizontal asympotote is y 1 and the vertical asymptote is x 2. Graph the rational function y 4 x 1 2 x 1 The vertical asymptote of a rational function is x -value where the denominator of the function is zero. Equate the denominator to zero and find the value of x.
To find oblique asymptotes the rational function must have the numerators degree be one more than the denominators which it is not. So there are no oblique asymptotes. Summing this up the asymptotes are y 0 and x 0.
To confirm this try graphing the function y 1x and zooming out very very far.