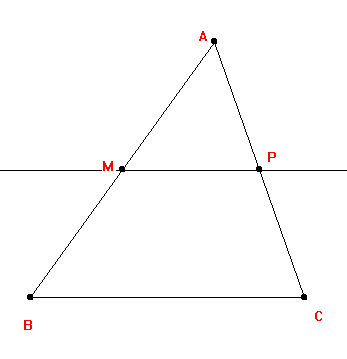
So x M y M 3 12 is the midpoint of the segment defined by A and B. In a right triangle the midpoint of the hypotenuse is equidistant from the three polygon vertices Dunham 1990.
This ellipse is centered at the triangles centroid and it has the largest area of any ellipse inscribed in the triangle.
Midpoint of a triangle. The midpoint formula is used to determine the midpoint between the two given points. If P 1 x 1 y 1 and P 2 x 2 y 2 are the coordinates of two given endpoints then the midpoint formula is given as. Midpoint x 1 x 22 y 1 y 22 The converse of MidPoint Theorem.
Take a square of paper. Put a mark half way along each side ABCD. You can do this easily by folding Join two midpoints DC as shown then mark half way along.
Draw the line between A and B and call it AB. Take the midpoint of AB and measure the distance from it to C. Draw a line twice that distance from C through ABs midpoint.
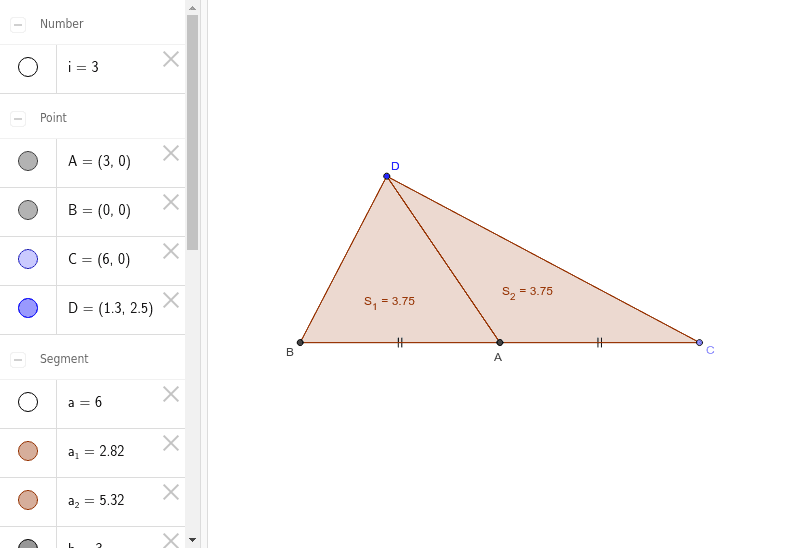
The end of that line is a corner of the original triangle call it P Repeat this for the other corners forming the points Q and R which are the vertices of the required triangle. To find the midpoint of a triangle known technically as its centroid follow these steps. Find the midpoint of the sides of the triangle.
If you know how to do this skip to step 5. Measure the distance between the two end points and divide the result by 2. The Midpoint Theorem states that the line segment joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of the third side.
Consider an arbitrary triangle ΔABC Δ A B C. Let D and E be the midpoints of AB and AC. Suppose that you join D and E.
The line segment connecting the midpoints of two sides of a triangle is parallel to the third side and is congruent to one half of the third side. Consider the triangle ABC with the midpoint of AB labelled M. Midpoint Of A Triangle Worksheets - there are 8 printable worksheets for this topic.
Worksheets are 3 the midpoint formula Geometry work medians cent. To answer what the midpoint of AB is simply replace the values in the formula to find the coordinates of the midpoint. In this case these are 2 4 2 3 and 6 18 2 12.
So x M y M 3 12 is the midpoint of the segment defined by A and B. In physics midpoint calculations have several prominent. Midpoint xM yM x M y M xA xB 2 yA yB 2 x A x B 2 y A y B 2 0 8 2 2 8 2 0 8 2 2 8 2 8 2 10 2 8 2 10 2 Midpoint of a line segment xM yM x M y M 4 5 Midpoint calculator uses coordinates of two points AxA yA A x A y A and BxB yB B x B y B in the two-dimensional Cartesian coordinate plane and find the halfway point between two given points A A and B B on a line segment.
The coordinates of that midpoint are 60. Then find the point that sits two-thirds of the way from the opposite vertex 39. Replace x1 x2 y1 and y2 with their respective values.
Replace k with 23. Simplify the computation to get the point. In this example the centroid is the point 53.
In a right triangle the midpoint of the hypotenuse is equidistant from the three polygon vertices Dunham 1990. In the figure above the trilinear coordinates of the midpoints of the triangle sides are and. The midpoint of a line segment with endpoints and given in trilinear coordinates is where 3.
Midpoint Of A Triangle - Displaying top 8 worksheets found for this concept. Some of the worksheets for this concept are 3 the midpoint formula Geometry work medians centroids 1 Midpoint formula es1 Midsegment of a triangle date period Practice a the triangle midsegment theorem Midpoint formula Performance based learning and assessment task distance Geometry honors coordinate geometry. The medial triangle or midpoint triangle of a triangle ABC is the triangle with vertices at the midpoints of the triangles sides AB AC and BC.
It is the n 3 case of the midpoint polygon of a polygon with n sides. The midsegment of a triangle is a line constructed by connecting the midpoints of any two sides of the triangle. It does not matter if you have a right triangle isosceles triangle or an equilateral triangle all three sides of a triangle can be bisected cut in two with the point equidistant from either vertex being the midpoint of that side.
OA 0b ON So 3 Total for Question 24 is 6 marks TOTAL FOR PAPER IS 100 MARKS 27 p 43383 A 02728 24 04B is a triangle. M is the midpoint of 014. N is the midpoint of OB.
0M m Show that AB is parallel to MN. 26 VE AS Diagram NOT accurately drawn Total for Question 24 is 3 marks. Every triangle has an inscribed ellipse called its Steiner inellipse that is internally tangent to the triangle at the midpoints of all its sides.
This ellipse is centered at the triangles centroid and it has the largest area of any ellipse inscribed in the triangle. In a right triangle the circumcenter is the midpoint of the hypotenuse. The mid-points of the sides of a triangle are 5 1 3 -5 and -5 -1.
Find the coordinates of the vertices of the triangle. The Midpoint Theorem Figure 1 shows Δ ABC with D and E as midpoints of sides AC and AB respectively. If you look at this triangle as though it were a trapezoid with one base of BC and the other base so small that its length is virtually zero you could apply the median theorem of trapezoids Theorem 55.