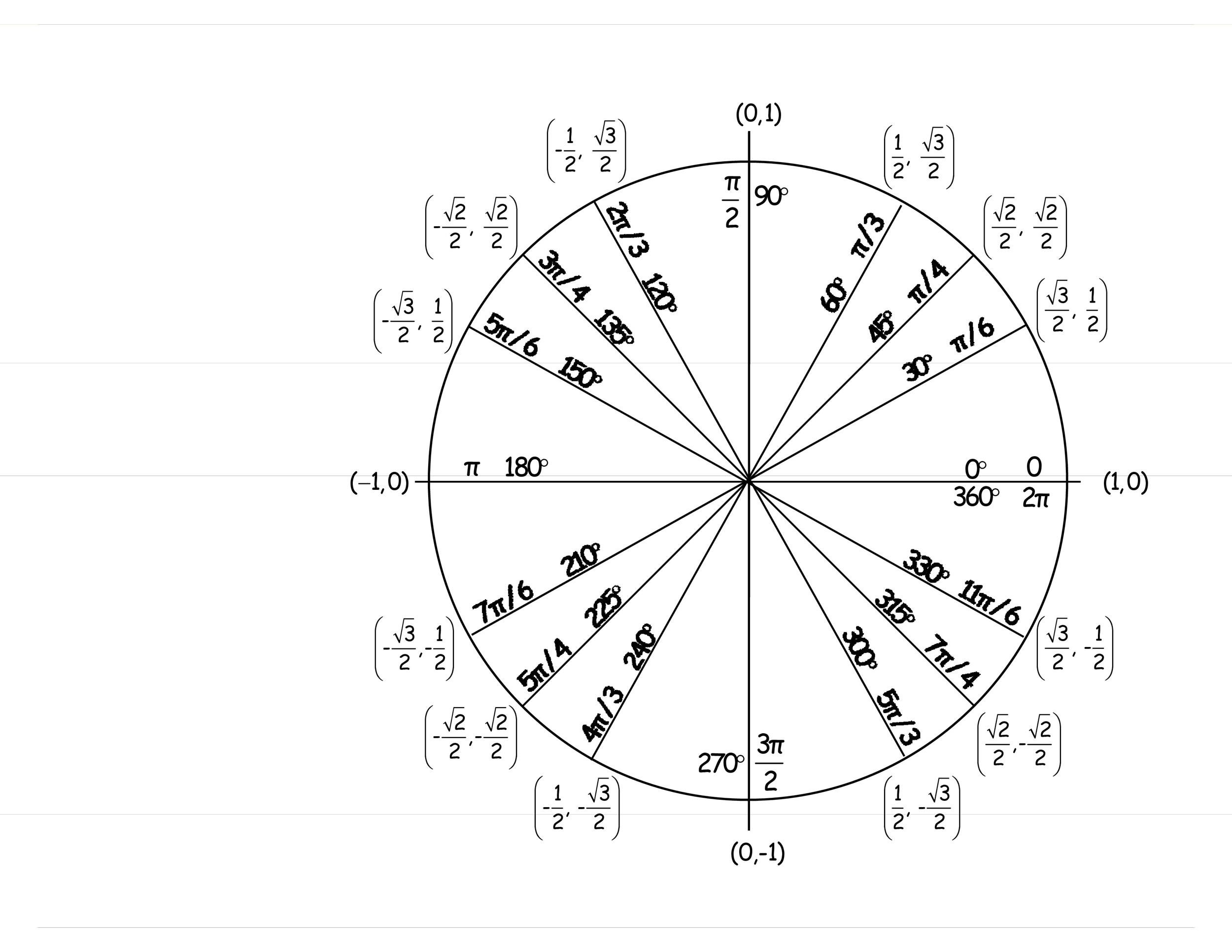
90 degrees has coordinates 0 1 on the unit circle. The above definition applies to negative angles also.

If we then rationalize the denominators we get.
Negative angles on unit circle. The unit circle is a platform for describing all the possible angle measures from 0 to 360 degrees all the negatives of those angles plus all the multiples of the positive and negative angles from negative infinity to positive infinity. In other words the unit circle shows you all the angles that exist. The unit circle is a platform for describing all the possible angle measures from 0 to 360 degrees all the negatives of those angles plus all the multiples of the positive and negative angles.
Enjoy the videos and music you love upload original content and share it all with friends family and the world on YouTube. Mar 14 2018 - This section contains. Angles in Trigonometry Degrees Radians and Co-Terminal Angles The Unit Circle More Practice Angles in Trigonometry Even though the word trigonometry is derived from the word triangle youll see a lot of circles when you work with Trig.
We talked about angle measures in the Introduction to Trigonometry section and now well. In trigonometry negative angles go clockwise. The above definition applies to negative angles also.
In the figure above drag the point clockwise. Note how the sine ratio still holds and produces values similar to those for positive angles. If the hypotenuse is made to be one unit long the trig functions all simplify.
Angle measurements start at 0 on the positive -axis and go counter-clockwise around the circle until they are back at 360 as shown in the graphs below. Remember from Geometry that there are 360 degrees 360 in a circle. When going clockwise from the positive -axis angles measurements are negative.
Here are some examples. I can create triangles on the unit circle using positive angles of rotation but do not know how to create a negative angle of rotation. If anyone could direct me to a good resource which would allow me to obtain my goal then I would be much obliged for a reply to this post.
Given a negative angle we add 360 to get its corresponding positive angle. When an angle is -360 it implies that the object made more than one cycle in clockwise direction. Find the corresponding positive angle of a -35 b -60 c -180 d - 670 2.
Find the corresponding negative angle of 80 167 330and 1300. Aside from positive angles unit or radian circle charts also show negative angles. In fact a lot of basic angles have negative values and multiples of themselves.
In order to get these values you need to measure the angles in a clockwise direction. For instance a 30-degree angle is the same as a -330-degree angle. The original angle A is in red and the negative angle -A is in blue.
The relationships between A and -A are the Negative Angle Identities catchy name right. Cos -A cos A sin -A - sin A. Negative theta by the way simply means that you measure the angle theta going clockwise from the original position rather than counterclockwise.
So for example if your theta is such that you wind up elsewhere on the unit circle like this point doesnt matter. The definition still holds. Using the unit circle diagram draw a line tangent to the unit circle where the hypotenuse contacts the unit circle.
This line is at right angles to the hypotenuse at the unit circle and touches the unit circle only at that point the tangent point. Extend this tangent line to the x-axis. Any angle can be viewed as a rotation from the positive direction of the axis of abscissas x axis toward a certain ray OM.
As such counterclockwise rotation is deemed positive and clockwise rotation is deemed negative. Vector OM connecting the origin with point M is called the radius vector of point M or the terminal side of the angle. At t π 4 or 45 degrees x y x x 1 2 1 2 x 1 2 y 1 2 cos t 1 2 sin t 1 2.
If we then rationalize the denominators we get. Cos t 1 22 2 2 2 sin t 1 22 2 2 2. Therefore the x y coordinates of a point on a circle of radius 1 at an angle of 45 are 2 2 2 2.
This trigonometry video tutorial explains how to find a positive and a negative coterminal angle given another angle in degrees or in radians using the unit. The one on the left goes counterclockwise and is defined to be a positive angle. The one on the right goes clockwise and is defined to be a negative angle.
If you used a protractor to measure the angles you would get 50 in both cases. We refer to the first one as a 50 angle and we refer to the second one as a angle. In many contexts an angle of θ is effectively equivalent to an angle of one full turn minus θ.
For example an orientation represented as 45 is effectively equivalent to an orientation represented as 360 45 or 315. However a rotation of 45 would not be the same as a rotation of 315. This time we dont need to find the positive corresponding acute angle.
90 degrees has coordinates 0 1 on the unit circle. Negative is the same as positive so its no surprise that sin is negative.