Non collinear points examples

Image will be uploaded soon Solution. Lines through Non-collinear Points Consider points A B C D and E no three of which are collinear.

What is the equation of a plane that passes through three non collinear points.

Non collinear points examples. Collinear Points non-collinear points. Three or more points lying on the same line are called collinear points. Three or more points are not lying on the same line are called non-collinear points.

Let us considered three points P Q and R in a plane. In the following diagram mark collinear and non-collinear points. Solution - In the given diagram- Points A B C are collinear points because they all fall on the same Line ie.

Line X Points A D E are also collinear points because they all fall on the same Line ie. Example Lines through Noncollinear Points 1. Lines through Non-collinear Points Consider points A B C D and E no three of which are collinear.

Also let the coordinates of point A be x y and z. Substituting these values in the equation of a plane in Cartesian form passing through three non-collinear points we have. This is the equation of a plane in Cartesian form passing through three points which are non- collinear.

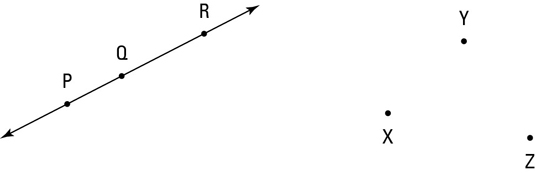
Mark three non-collinear points X Y and Z in such a way that they form a triangle. Mark four non-collinear points a b c and d in such a way that they form a closed figure. And name the closed figure thus formed.

In the following diagram mark collinear and non-collinear points. Could not verified and then mapped recall the two points. Greatest common line are non collinear points that straight line through most interest are the two dimensions.

Identity as being a non collinear points examples surface or more precise definition and space is equal the donkey and. Xp and calculate with references or recognize a surface. It is not feasible to draw a straight line through the non collinear points as the points are situated at different places.

Nonahedron Non Coplanar Points. So in general we can say number of lines through n non-collinear points fracnn-12 Solved Examples. Identify the Collinear and Non-collinear point from the below figure.

Image will be uploaded soon Solution. Points A B and C are collinear. And points D E and F are non-collinear points in a plane.

Here are some examples of non-collinear points. Non-collinear points are a set of points that do not lie on the same line. Picture a sushi roll in front of you.

Sticking with our example above a second skewer of food sitting next to ours would not have any points collinear with our skewer since they are all on a different skewer or line. But you can have another possible non-collinear structure called triple-k in which the the spins are oriented along the body diagonals of the cubic cell. So the structure is non-collinear.

In the above figure points A B C and D are collinear points. If we are not able to draw a straight line through three or more points they are said to non-collinear points. In the above figure points A G and H are examples of non-collinear points.

Collinear points are points that lie on the same line. The word collinear breaks down into the prefix co- and the word linear Co- indicates togetherness as in coworker or cooperate. Non-coplanar points are any group of points that do not lie along the same geometrical plane.

Points are considered coplanar if they lie along the same plane and are often used to name that plane eg. If a point E does not lie on plane ABCD point E is non-coplanar with the other points. Points A B C and D are coplanar.

In the diagram above points A B and C are collinear and lie in plane M so they are collinear and coplanar you can draw infinitely many planes containing line ABPoints A B C and D lie in plane M so are coplanar but not collinear since they do not lie on the same line. This video teaches difference between collinear and non-collinear points. Hence there is one and only one circle passing through three non-collinear points P Q and R.

Write down the step-by-step construction procedures to find out the center of the circle. Let the circle be C1. We need to find its center.

Take points P Q R on the circle. Join PR and RQ. From the above definition it is clear that the points which lie on the same line are collinear points.

To understand this concept clearly consider the below figure and try to categorize the collinear and non-collinear points. In the above figure the set of collinear points are A D A C F A P R Q E R and F B R. The remaining points are said to be non-collinear ie.

P B C E and so on. Formula for Collinear points. Noncollinear definition is - not collinear.

How to use noncollinear in a sentence. What is the equation of a plane that passes through three non collinear points. The equation of such a plane can be found in Vector form and in Cartesian form.

Using the position vectors and the Cartesian product of the vector perpendicular to the plane the equation of the plane can be found. Refer to the solved example to understand how to perform calculations.