Orthocenter of a triangle

Orthocenter of a triangle. Note that the altitudes intersect in a single point.

It can be shown that the altitudes of a triangle are concurrent and the point of concurrence is called the orthocenter of the triangle.

Orthocenter of a triangle. The orthocenter is not always inside the triangle. If the triangle is obtuse it will be outside. To make this happen the altitude lines have to be extended so they cross.

Adjust the figure above and create a triangle where the orthocenter is outside the triangle. Follow each line and convince yourself that the three altitudes when extended the right way do in fact intersect at the orthocenter. Summary of triangle centers There are many types of triangle centers.

The orthocenter is one of the triangles points of concurrency formed by the intersection of the triangle s 3 altitudes. These three altitudes are always concurrent. In other the three altitudes all must intersect at a single point and we call this point the orthocenter of the triangle.

Sides – Three sides intersecting at vertices forming three interior angles. Altitudes – The line segment from each vertex of the triangle to the opposite side or extension of the opposite side that is perpendicular to that. Orthocenter – The intersection of the three altitudes.

Orthocenter of a triangle. Create the altitude from each vertex of the triangle. The altitude is the segment from a vertex perpendicular to the opposite side.

Sometimes the altitude may be outside the triangle. Note that the altitudes intersect in a single point. The orthocenter of a triangle is the intersection of the triangles three altitudes.

It has several important properties and relations with other parts of the triangle including its circumcenter incenter area and more. The orthocenter is typically represented by the letter. In a right triangle the orthocenter is the polygon vertex of the right angle.

When the vertices of a triangle are combined with its orthocenter any one of the points is the orthocenter of the other three as first noted by Carnot Wells 1991. These four points therefore form an orthocentric system. The orthocenter of the triangle is usually denoted by H which is the intersection point of three altitudes of a triangle.

Where the triangles three altitudes intersect. The altitude of a triangle is a segment from a vertex of the triangle to the opposite side or to the extension of the opposite side if necessary thats perpendicular to the opposite side. The opposite side is called the base.

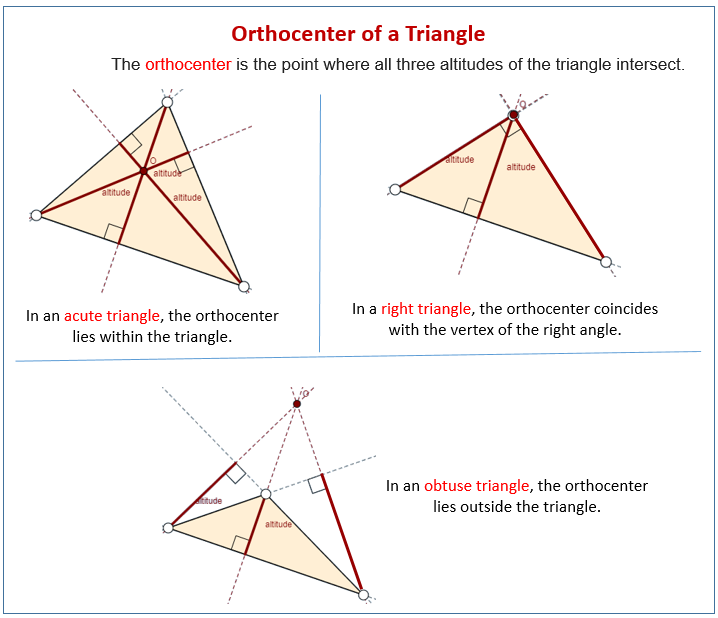
The orthocenter is the point where all three altitudes of the triangle intersect. An altitude is a line which passes through a vertex of the triangle and is perpendicular to the opposite side. There are therefore three altitudes in a triangle.

It can be shown that the altitudes of a triangle are concurrent and the point of concurrence is called the orthocenter of the triangle. The orthocenter is denoted by O. Let ABC be the triangle ADBE and CF are three altitudes from A B and C to BC CA and AB respectively.

Orthocenter Definition and How to Find with Example Orthocenter of a triangle is the intersection point of three altitudes drawn from the vertices to the opposite side. Learn its formula with solved examples and construction method at BYJUS. The three possibly extended altitudes intersect in a single point called the orthocenter of the triangle usually denoted by H.

The orthocenter lies inside the triangle if and only if the triangle is acute ie. Does not have an angle greater than or equal to a right angle. If one angle is a right angle the orthocenter coincides with the vertex at the right angle.

The orthocenter is the intersecting point for all the altitudes of the triangle. The point where the altitudes of a triangle meet is known as the Orthocenter. In the below mentioned diagram orthocenter is denoted by the letter O.

There is no direct formula to calculate the orthocenter of the triangle. The point where the altitudes of a triangle meet is known as the Orthocenter. It lies inside for an acute and outside for an obtuse triangle.

Altitudes are nothing but the perpendicular line AD BE and CF from one side of the triangle either AB or BC or CA to the opposite vertex. Orthocenter of Triangle Altitude Calculator Triangle orthocenter calculator is used to calculate the orthocenter point of a triangle. In geometry an orthocentric system is a set of four points on a plane one of which is the orthocenter of the triangle formed by the other three.

If four points form an orthocentric system then each of the four points is the orthocenter of the other three. These four possible triangles will all have the same nine-point circle. The three altitudes of any triangle are concurrent line segments they intersect in a single point and this point is known as the orthocenter of the triangle.

The steps to find the coordinates of the orthocenter of a triangle are relatively simple given that we know the coordinates of the vertices of the triangle. This geometry video tutorial explains how to identify the location of the incenter circumcenter orthocenter and centroid of a triangle. The incenter can b.