Parts of an ellipse

π a b. Its endpoints are the major axis vertices with coordinates h pm a k.

The a and the b have to do with how wide and how tall the ellipse is.

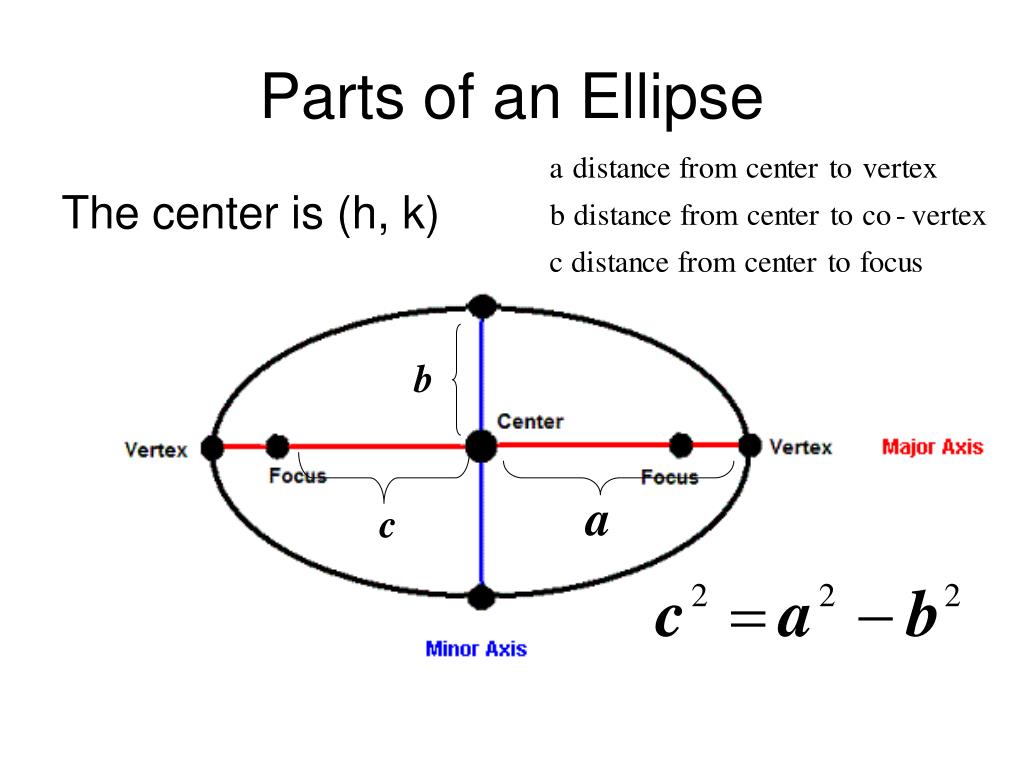
Parts of an ellipse. Parts of an Ellipse Center. The center of the ellipse has coordinates hk. The major axis of the ellipse is the longest width across it.

For a horizontal ellipse that axis is parallel to the x-axis. The major axis has length 2a. Its endpoints are the major axis vertices with coordinates h pm a k.

The area of an ellipse is. π a b. Where a is the length of the Semi-major Axis and b is the length of the Semi-minor Axis.

A and b are from the center outwards not all the way across. For a circle a and b are equal to the radius and you get π r r πr2 which is right. Key Takeaways Equation of an Ellipse.

An ellipse is a conic section formed by the intersection of a plane with a right circular cone. Parts of an Ellipse. The major axis of the ellipse is the longest width across it.

The minor axis of the ellipse is the. Parts of an Ellipse. These can be located using radical coordinates.

ON INSIDE OR OUTSIDE. A study in inequalities related to an ellipse. Powered by Create your own unique website with customizable templates.

An ellipse is the set of all points xy x y in a plane such that the sum of their distances from two fixed points is a constant. Each fixed point is called a focus plural. Foci of the ellipse.

We can draw an ellipse using a piece of cardboard two thumbtacks a pencil and string. Ellipses appear as plane sections of the following quadrics. Ellipsoid Elliptic cone Elliptic cylinder Hyperboloid of one sheet Hyperboloid of two sheets.

An ellipse is the technical name for an oval. Lets start by looking at the pattern of the ellipse and some key terms. There are two patterns for an ellipse.

In both patterns h k is the center point just as it was with a circle. The a and the b have to do with how wide and how tall the ellipse is. Each ellipse has a major axis and a minor.

Ellipses An ellipsis is a set of three periods indicating an omission. Each period should have a single space on either side except when adjacent to a quotation mark in which case there should be no space. Each type of ellipse has these main parts.

The point in the middle of the ellipse is called the center and is named h v just like the vertex of a. The major axis is the line that runs through the center of the ellipse the long way. The variable a is the.

The only difference between the circle and the ellipse is that in an ellipse there are two radius measures one horizontally along the x-axis the other vertically along the y-axis. Clearly for a circle both these have the same value. By convention the y radius is usually called band the x radius is called a.

Ellipses centered at the origin. 101 Two-circle construction for an ellipse Divide the circles into any number of parts. The parts do not necessarily have to be equal.

The radial lines now cross the inner and outer circles. Where the radial lines cross the outer circle draw short lines parallel to the minor axis CD. The Ellipse An Ellipse is the geometric place of points in the coordinate axes that have the property that the sum of the distances of a given point of the ellipse to two fixed points the foci is equal to a constant which we denominate 2a 2a.

Ellipse is defined by its two-axis along x and y-axis. The major axis is the longest diameter of the ellipse usually denoted by a going through the center from one end to the other at the broad part of the ellipse. Whereas the minor axis is the shortest diameter of ellipse denoted by b crossing through the center at the narrowest part.

Define b by the equations c 2 a 2 b 2 for an ellipse and c 2 a 2 b 2 for a hyperbola. For a circle c 0 so a 2 b 2. For the parabola the standard form has the focus on the x-axis at the point a 0 and the directrix is the line with equation x a.

In standard form the parabola will always pass through the origin. The longest diameter of an ellipse is known as the major axis. It extends from one side of the ellipse and passes through the center to the other side.

It is the diameter of the wider region of the ellipse. In other words the major axis coincides with the major diameter and passes through the center point and both foci. If x0y0 is the center of the ellipse if a and b are the two semi-axis lengths and if p is the counterclockwise angle of the a-semi-axis orientation with respect the the x-axis then the entire ellipse can be represented parametrically by the equations x x0 acos pcos t - bsin psin t.

Diagram of an ellipse that can used to illustrate the different parts. Segment MN is the major axis segment CD is the conjugate minor axis and point O is the center of the ellipse. Both foci are also labeled in the illustration.

I want the ellipse stroke to trim or hide in the portion behind the grey so that when I hide the grey text layers the circle has a padding from intersecting with the original white text. Note the text and offset path have an effect of arc lower and are in their own group. How I arrived here.

1 Ellipse tool with stroke and zero fill.