Properties of a rectangle diagonals

Properties of the diagonals of a rectangle. Finding length of MZ.

Each interior angle is equal to 90 degrees.

Properties of a rectangle diagonals. Properties of the diagonals of a rectangle. As you can see from the pictures to the left the diagonals of a rectangle do not intersect in a right angle they are not perpendicular. Unless the rectangle is a square And the angles formed by the intersection are not always the same measure size.

Since the diagonals of a rectangle are congruent MO 26. Finding length of MZ. To find MZ you must remember that the diagonals of a parallelogram bisect each otherRemember a rectangle is a type of parallelogram so rectangles get all of the parallelogram properties If MO 26 and the diagonals bisect each other then MZ ½26 13.

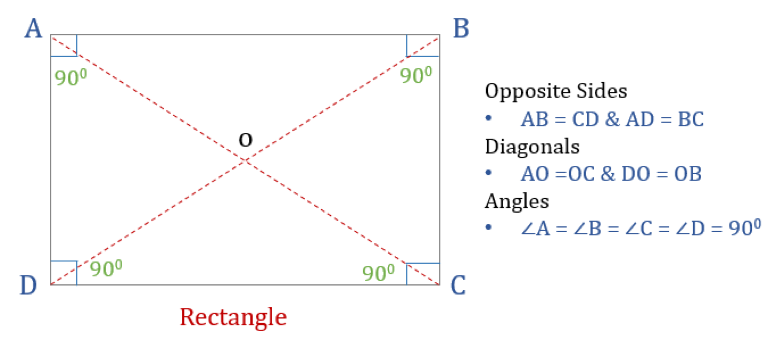
A rectangle has two diagonals. Each one is a line segment drawn between the opposite vertices corners of the rectangle. The diagonals have the following properties.

The two diagonals are congruent same length. In the figure above click show both diagonals then drag the orange dot at any vertex of the rectangle and convince yourself this is so. The properties of diagonals of rectangle is hereunder.

The diagonals of a rectangle are of the same length and intersect one another The two diagonals of a rectangle intersect each other at different angles one acute angle and the other an obtuse angle. A rectangle whose two diagonals intersect each other at right angles is known as a square. Now let us learn the properties of rectangle in this article.

The fundamental properties of rectangles are. A rectangle is a quadrilateral. The opposite sides are parallel and equal to each other.

Each interior angle is equal to 90 degrees. The sum of all the interior angles is equal to 360 degrees. The diagonals bisect each other.

The Diagonals of a Rectangle Are of Equal Length. Properties of a Square. The diagonals of a square are perpendicular bisectors of each other.

Introduction to Practical Geometry. Constructing a Quadrilateral When the Lengths of Four Sides and a Diagonal Are Given. The fundamental definition of a rectangle is as follows.

A rectangle is a quadrilateral whose interior angles are all equal. Since the sum of the interior angles of a polygon is. 360circ 360 it follows that each of the interior angles is a right angle.

Diagonal of a Rectangle. A rectangle has two diagonals that bisects each other. Both the diagonals are equal in length.

The rectangle is a symmetrical shape and has both the diagonals equal in length. A diagonal will divide the rectangle into two right angle triangles. Diagonals that are perpendicular and congruent diagonals that bisect opposite angles consecutive angles that are supplementary.

Play this game to review Geometry. The diagonals of a rectangle are Preview this quiz on Quizizz. The diagonals of a rectangle are.

The basic properties of a rectangle Rectangle can be a parallelogram rhombus or square in which all the angles right. An opposite sides of the rectangle are the same length ie. A rectangle has three properties.

All the angles of a rectangle are 90 Opposite sides of a rectangle are equal and Parallel. Diagonals of a rectangle bisect each other. Rectangle formula â Area and perimeter of a rectangle.

Remember that a 90 degree angle is called a. The diagonals of a rectangle bisect each other and are of the same length. The two diagonals of a rectangle bisect each other at different angles one obtuse angle and the other an acute angle.

A rectangle whose two diagonals bisect each other at right angles is called a square. Presented here are printable worksheets based on the next important property of the rectangle - the diagonals of a rectangle are congruent and bisect each other. Students of 5th grade and 6th grade need to apply the property to find the missing measure.

Rectangles are similar to squares. Therefore they also have two diagonals. Their diagonals are also congruent to each other and bisect each other.

Two congruent right triangles are obtained if the diagonal bisects a rectangle. In a rectangle all the angles are equal to 90º. On applying Pythagoras theorem in Δ ABD AB2 AD2 DB2 242 72 DB2 576 49 DB2 DB2 625 DB 25 cm Thus the length of the diagonal is 25 cm.

Properties of a Rectangle Opposite sides are parallel and congruent. All angles are right. The diagonals are congruent and bisect each other divide each other equally.

A rectangle is a parallelogram with each of the angles a right angle. Some of the properties of rectangles ar. Learn how to solve problems with rectangles.

A rectangle is a parallelogram.