Rotational kinetic energy equation

1 Now Σmr 2 is known as moment of inertia I which is the rotational equivalent of mass or inertia. Kinetic energy is the energy of moving objects including objects that are rotating.

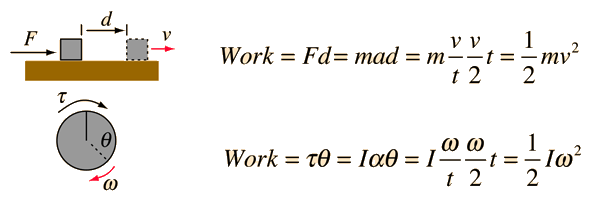
The angular kinetic energy is directly proportional to the mass of the rotating object.

Rotational kinetic energy equation. The Formula for Rotational Kinetic Energy We can compute it with the following Rotational Kinetic Energy Formula. Energy frac12 times moment. Inertia times angular.

Rotational Kinetic Energy Dimensional Formula. We know that rotational kinetic energy is given as. K R frac12 I ω 2.

Rotational kinetic energy K R frac12 Moment of inertia Angular velocity 2 Dimensional formula of moment of inertia M 1 L 2 T 0. Dimensional formula of angular velocity M 0 L 0 T-1. The angular kinetic energy is directly proportional to the mass of the rotating object.

The position of the point mass from the axis of rotation also determines its energy. The particles that are further from the rotation axis possess more rotational kinetic energy than the ones closer to the rotational axis. The Formula for Rotational Energy.

For spinning objects you have to convert from the linear concept of kinetic energy to the rotational concept of kinetic energy. You can calculate the kinetic energy of a body in linear motion with the following equation. Where m is the mass of the object and v is the speed.

Rotational kinetic energy can be expressed as. Erotational 1 2I ω2 E rotational 1 2 I ω 2 where ω ω is the angular velocity and I I is the moment of inertia around the axis of rotation. The mechanical work applied during rotation is the torque times the rotation angle.

W τ θ W τ θ. The instantaneous power of an angularly accelerating body. The angular acceleration is equal to the final angular velocity divided by the time and the average angular velocity is equal to half the final angular velocity.

It follows that the rotational kinetic energy given to the flywheel is equal to the work done by the torque. This result shows that the larger the value of c the slower the object is because a larger fraction of the potential energy is directed toward the rotational kinetic energy with less available for the translational kinetic energy and so the object moves translates more slowly. Simulation 2 1 gh v c Mgh ½Mv2 ½cMv2.

The objects rotational kinetic energy is the sum of the kinetic energies of all the particles. K rot ½ m 1 ω 2 r 1 2 ½ m 2 ω 2 r 2 2. ½ Σmr 2 ω 2.

1 Now Σmr 2 is known as moment of inertia I which is the rotational equivalent of mass or inertia. Thus the Rotational Kinetic Energy ½ I ω 2 2. Substituting Equation 1052 into Equation 1051 the expression for the kinetic energy of a rotating rigid body becomes 1053 K 1 2 I ω 2.

We see from this equation that the kinetic energy of a rotating rigid body is directly proportional to the moment of inertia and the square of the angular velocity. The expression for rotational kinetic energy is exactly analogous to translational kinetic energy with I being analogous to m and ω to v. Rotational kinetic energy has important effects.

Flywheels for example can be used to store large amounts of rotational kinetic energy in a vehicle as seen in Figure 3. Rotational Kinetic Energy 2-1 Moment of Inertia Angular velocity 2 Or RK e M 1 L 2 T 0 M 0 L 0 T -1 2 M 1 L 2 T -2. Therefore rotational kinetic energy is dimensionally represented as M 1 L 2 T -2.

Rotational Kinetic Energy Formula The following equation is used by the calculator to determine the rotational kinetic energy of an object. E 05 I ω² Where E is the rotational kinetic energy in Joules. Rotational energy occurs due to the objects rotation and is a part of its total kinetic energy.

If the rotational energy is considered separately across an objects axis of rotation the moment of inertia is observed. Rotational Kinetic Energy Formula. Rotational kinetic energy K frac12 Iω².

Where K is Rotational Kinetic. Rotational energy or angular kinetic energy is kinetic energy due to the rotation of an object An example is the calculation of the rotational kinetic energy of the Earth. As the Earth has a period of about 2393 hours it has an angular velocity of.

To finish off our comparison of translational straight-line and rotational motion lets consider the rotational equivalent of momentum which is angular momentum. For straight-line motion momentum is given by p mv. Momentum is a vector pointing in the same direction as the velocity.

Angular momentum has the symbol L and is given by the equation. The moment of inertia I 1 kg m2 The angular velocity ω 2 rads Wanted. The rotational kinetic energy KE.

Kinetic energy is the energy of moving objects including objects that are rotating. The kinetic energy of a rotating object depends on the objects angular rotational velocity in radians per second and on the objects moment of inertia. Moment of inertia is a measure of how easy it is to change the rotation of an object.

An example is the calculation of the rotational kinetic energy of the Earth. As the Earth has a period of about 2393 hours it has an angular velocity of 72910 5 rads. The Earth has a moment of inertia I 80410 37 kgm 2.

Therefore it has a rotational kinetic energy of 213810 29 J.