Solving multiple angle trigonometric equations

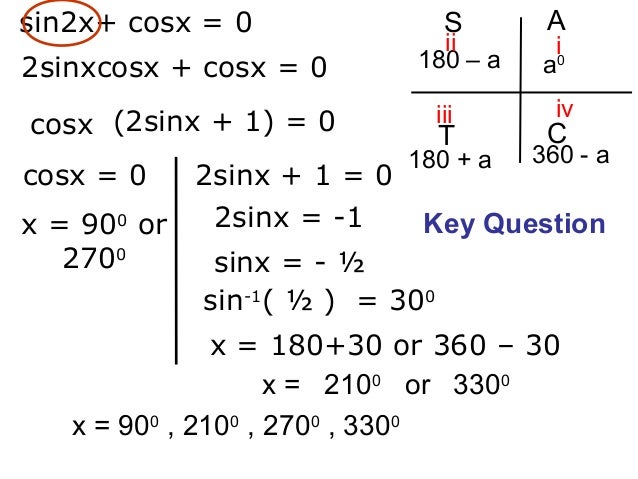
Determining non-permissible values for trig expressions. By using this website you agree to our Cookie Policy.

So we must adjust it for the new angle.

Solving multiple angle trigonometric equations. I continue my examples of solving algebraic equations that involve multiple angles such as sin2x. There you will find. I continue my examples of solving algebraic equations that involve.

63 Trig Equations with Multiple Angles When solving trig equations where the angle is something other than x or θ you MUST adjust the interval. Solve the equation over the interval 02 π 1 sin 2 2 x The given interval is 0 2. So we must adjust it for the new angle.

0 2 2 2 2 x π which is 0 2 x π 2. This trigonometry video tutorial shows you how to solve trigonometric equations using identities with multiple angles by factoring and by finding the gener. Solving first degree trigonometric equations.

Determining non-permissible values for trig expressions. Solving second degree trigonometric equations. Solving trigonometric equations involving multiple angles.

Solving trigonometric equations using pythagorean identities. Solving trigonometric equations using sum and difference. Equations with multiple angles in a given range care must be taken not to fall into common mistakes.

In this video I show you how the quadrant rule can be used to solve these types of questions. I am assuming that you have seen the earlier video on the quadrant rule. Solving a Multiple Angle Trigonometric Equation Solve exactly.

Latexcos left2xrightfrac12latex on latexleft02pi rightlatex. Sometimes it is not possible to solve a trigonometric equation with identities that have a multiple angle such as or When confronted with these equations recall that is a horizontal compression by a factor of 2 of the function On an interval of we can graph two periods of as opposed to one cycle of This compression of the graph leads us to believe there may be twice as many x-intercepts or solutions to compared to This information will help us solve the equation. Solving Trigonometric Equations with Multiple Angles.

Sometimes it is not possible to solve a trigonometric equation with identities that have a multiple angle such as sin2x or cos3x. When confronted with these equations recall that ysin2x is a horizontal compression by a factor of 2 of the function ysin x. Solving Trigonometric Equations with Multiple Angles.

Sometimes it is not possible to solve a trigonometric equation with identities that have a multiple angle such as sin 2 x sin 2 x or cos 3 x. When confronted with these equations recall that y sin 2 x y sin 2 x is a horizontal compression by a factor of 2 of the function y sin x. Y sin x.

Free trigonometric equation calculator - solve trigonometric equations step-by-step This website uses cookies to ensure you get the best experience. By using this website you agree to our Cookie Policy. We have to be careful when solving trig equations with multiple angles meaning there is a coefficient before the x or theta variable.

This is because we could have fewer or more solutions in the Unit Circle and thus for all real solutions when we add the 2pi k or pi k. Solving Trigonometric Equations with Multiple Angles. When confronted with trigonometric equations that have a multiple angle such as sin2x or cos3x recall that ysinBx is a horizontal compression by a factor of B of the function ysin x.

Also we are going to look at an incredibly powerful trick for solving multiple angle or half-angle equations it takes the sting right out of it I promise. Yes as Purple Math states you will need to put your thinking cap on because sometimes your first instinct doesnt get you any closer to a desired outcome but taking a different. When the trigonometric equation involves a multiple angle the trigonometric equation is evaluated first and then the multiple of the angle is then divided through the obtained answer.

Solving trig equations including multiple angles using identities. Trigonometry from Greek trigōnon triangle and metron measure is a branch of mathematics that studies relationships between side lengths and angles of triangles. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies.

What follows are illustrations of dealing with trig equations with multiple angles. Equation with a Half -angle Example. Solve 2 3 sin 2 3 over the interval 0360.

Write the interval 0360 as an inequality 0 360 0 2 180 and set up the equation 2 3 sin 2 3 sin 2 3 2 3 sin 2 3 2 2 60120 120240 and write the. This video goes through a couple examples of how to solve a trigonometric equation involving multiple angles.