Tangent secant power theorem

If a tangent and a secant or a chord intersect on a circle at the point of tangency then the measure of the angle formed is _____ the measure of its. Remember that this theorem only used the intercepted arcs.

Length of a tangent segment using tangent - secant power theorem.

Tangent secant power theorem. The tangent-secant theorem describes the relation of line segments created by a secant and a tangent line with the associated circle. This result is found as Proposition 36 in Book 3 of Euclids Elements. This geometry video tutorial provides a basic introduction into the power theorems of circles which is based on chords secants and tangents.

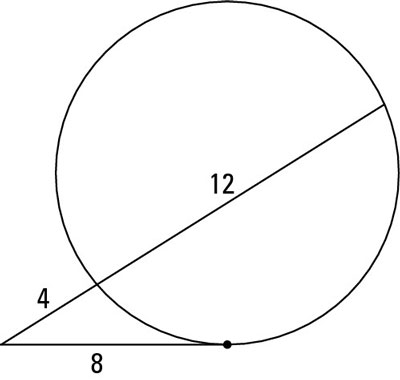
You can solve some circle problems using the Tangent-Secant Power Theorem. This theorem states that if a tangent and a secant are drawn from an external point to a circle then the square of the measure of the tangent is equal to the product of the measures of the secants external part and the entire secant. Secant-Tangent Power Theorem If a tangent and a secant intersect in the exterior of a circle then the square of the measure of the tangent is equal to the product of the measures of the secant and its external secant segment.

PM2 PNcdot PO. Using the Tangent-Chord Theorem it is simple to prove the third theorem which provides a relationship between lines in circles - the Tangent-Secant Theorem the other two being the Intersecting Secants Theorem and the Intersecting Chords Theorem. AB is tangent to circle O and AC is a secant line intersecting the circle at points C and D.

Prove that AB 2 AC AD. 0020 - Definition of tangent and secant line 0347 - Theorems on Tangent line 1002 - Theorems on Angle Formed By Tangent And Secant 2449 - Solve Problems Involving Theorems on Angle Formed By tangent and secant 4642 - Power Theorem Theorems on Chords Tangents and Secant Segments Power Theorems Theorems on Chord Tangent and Secant Segments. Tangent Secant Segment Theorem.

If a tangent and a secant are drawn from a common point outside the circle and the segments are labeled like the picture to the left then. This means that the product of the outside segment of the secant and the whole is equal to the square of the tangent segment. Finding the Value of a Missing Segment 1.

Tangent and Secant The measure of an angle formed by a secant and a tangent drawn from a point outside the circle is 1 2 the difference of the intercepted arcs. Remember that this theorem only used the intercepted arcs. Therefore the red arc in the picture below is not used in this formula.

Length of a tangent segment using tangent - secant power theorem. Length of tangent segment using tangent-tangent power theorem. Length of tangent segment using tangent-tangent power theorem.

Measure of an angle with vertex is on the circle chord and chord. About 23 results 036 milliseconds. If a tangent and a secant or a chord intersect on a circle at the point of tangency then the measure of the angle formed is _____ the measure of its.

If a secant and a tangent of a circle are drawn from a point outside the circle then the product of the lengths of the secant and its external segment equals the square of the length of the tangent segment. Power of a point with a tangent segment and a secant segment. Tangent - secant demonstration Demonstration of a circle geometry property Tangent Secant Theorem with quadratic expressions - Geometry This video focuses on using the Tangent Secant Theorem to find the length of a tangent line segment.

This video also reviews how to find the roots. The Tangent-Secant Theorem represents that if a line from a point D outside a circle intersects the circle at exactly one point C in other words DC is tangent to the circle and a secant a line intersecting the circle at two points from the same external point D meets the circle at points G and E respectively then DC 2 DG DE as shown in the diagram. This equality is sometimes known as the secant-tangent theorem intersecting chords theorem or the power-of-a-point theorem.

In the case that P lies inside the circle the two points of intersection will be on different sides of the line through P. The line can be considered to have a direction so that one of the distances is negative and therefore so is the product of the two. A secant of a circle is a line connecting two points on the circle.

A tangent to a circle is a line that intersects a circle exactly once. When a nonparallel tangent and secant are given their intersection point satisfies a key property. The third case of the power of a point theorem.

Intersecting Secant-Tangent Theorem If a tangent segment and a secant segment are drawn to a circle from an exterior point then the square of the measure of the tangent segment is equal to the product of the measures of the secant segment and its external secant segment. In the circle U V is a tangent and U Y is a secant. Relationship to Tangent-Secant Theorem In the figure above drag point B around the top until it meets point A.

The line is now a tangent to the circle and PAPB. Since PAPB then their product is equal to PA 2. PA 2 PCPD This is the Tangent-Secant Theorem.