Vertices of an ellipse

Perimeter of an Ellipse. The vertices of an ellipse are the points on the ellipse that are the farthest distance horizontally from one another and the farthest distance vertically from one another.

Here the vertices of the ellipse are.

Vertices of an ellipse. Learn how to graph vertical ellipse not centered at the origin. A vertical ellipse is an ellipse which major axis is vertical. To graph a vertical ellipse w.

The points of intersection of the ellipse and its major axis are called its vertices. Here the vertices of the ellipse are A a 0 and A a 0. Co-vertices are B 0b and B 0 -b.

Vertices of an Ellipse. The points at which an ellipse makes its sharpest turns. The vertices are on the major axis the line through the foci.

Vertex directrices of an ellipse vertices of a hyperbola vertex of a parabola. This page updated 19-jul-17 Mathwords. Terms and Formulas from Algebra I to Calculus.

The standard form of an ellipse in Cartesian coordinates assumes that the origin is the center of the ellipse the x-axis is the major axis and. The foci are the points the vertices are. For an arbitrary point the distance to the focus is and to the other focus Hence the point is on the ellipse whenever.

Vertices of ellipse A 1 A 2 B 1 B 2. Diameter of ellipse - is any straight line segment that passes through the center of the ellipse and whose endpoints lie on the ellipse. Linear eccentricity c - is the distance from the focal point to the center of the ellipse.

An ellipse is the locus of all those points in a plane such that the sum of their distances from two fixed points in the plane is constant. The fixed points are known as the foci singular focus which are surrounded by the curve. The fixed line is directrix and the constant ratio is eccentricity of ellipse.

Eccentricity is a factor of the ellipse which demonstrates the elongation of it. An ellipse is a part of a conic section that is formed when we cut a cone at an angle. It is a locus of a point that moves in such a manner so that the ratio of distances from a fixed.

Free Ellipse Vertices calculator - Calculate ellipse vertices given equation step-by-step This website uses cookies to ensure you get the best experience. By using this website you agree to our Cookie Policy. Perimeter of an Ellipse.

On the Ellipse page we looked at the definition and some of the simple properties of the ellipse but here we look at how to more accurately calculate its perimeter. Rather strangely the perimeter of an ellipse is very difficult to calculate. There are many formulas here are some interesting ones.

-The vertices are 4 units above and below the center. -The foci are sprt7 units above and below the center. An ellipse has a center at the origin a vertex along the major axis at 13 0 and a focus at 12 0.

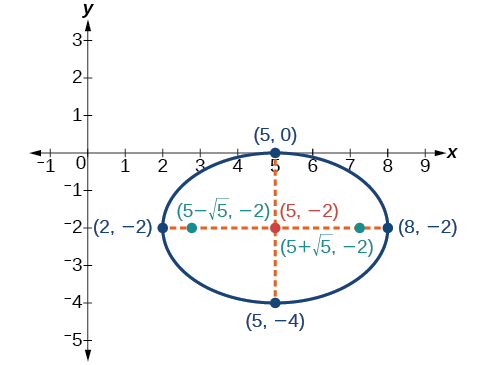
Use the standard forms of the equations of an ellipse to determine the major axis vertices co-vertices and foci. Solve for c c using the equation c2 a2 b2 c 2 a 2 b 2. Plot the center vertices co-vertices and foci in the coordinate plane and draw a smooth curve to form the ellipse.

The vertices of an ellipse are the points on the ellipse that are the farthest distance horizontally from one another and the farthest distance vertically from one another. The points of intersection of the ellipse and its major axis are called its vertices. Here the vertices of the ellipse are.

Aa 0 and A a 0. It is a focal chord perpendicular to the major axis of the ellipse. The equations of latus rectum are x ae x ae.

E 1 - b 2 a 2 Directrix. A vertical ellipse is an ellipse which major axis is vertical. When the equation of an.

Learn how to graph vertical ellipse which equation is in general form. Each endpoint of the major axis is the vertex of the ellipse plural. Vertices and each endpoint of the minor axis is a co-vertex of the ellipse.

The center of an ellipse is the midpoint of both the major and minor axes. This calculator will find either the equation of the ellipse standard form from the given parameters or the center vertices co-vertices foci area circumference perimeter focal parameter eccentricity linear eccentricity latus rectum length of the latus rectum directrices semimajor axis length semiminor axis length x-intercepts y-intercepts domain and range of the. This is true for any point on the ellipse.

Axes of an ellipse. The midpoint C of the line segment joining the foci is the center of the ellipse. The chord through the foci is the major axis of the ellipse and the chord perpendicular to it through the center is the minor axis.

The endpoints of the major axis are called vertices.